Câu hỏi
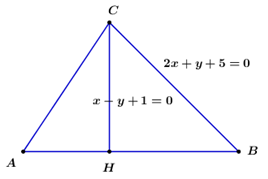
Cho tam giác \(ABC\) có \(A\left( {1; - 2} \right),\) đường cao \(CH:\;\;x - y + 1 = 0,\) đường thẳng chứa cạnh \(BC\) có phương trình \(2x + y + 5 = 0.\) Tọa độ điểm \(B\) là:
- A \(\left( {4;\;3} \right)\)
- B \(\left( {4; - 3} \right)\)
- C \(\left( { - 4;\;3} \right)\)
- D \(\left( { - 4; - 3} \right)\)
Phương pháp giải:
Ta có: \(CH \bot AB \Rightarrow \) lập được phương trình đường thẳng đi qua \(A\) và vuông góc với \(CH.\)
Khi đó tọa độ điểm \(B\) là nghiệm của hệ phương trình gồm phương trình đường thẳng \(BC\) và \(AB.\)
Lời giải chi tiết:
Ta có: \(CH \bot AB \Rightarrow \) lập được phương trình đường thẳng \(AB\) đi qua \(A\) và vuông góc với \(CH\) là:
\(x - 1 + y + 2 = 0 \Leftrightarrow x + y + 1 = 0.\)
\( \Rightarrow \left\{ B \right\} = AB \cap BC \Rightarrow \) tọa độ điểm \(B\) là nghiệm của hệ phương trình: \(\left\{ \begin{array}{l}2x + y + 5 = 0\\x + y + 1 = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = - 4\\y = 3\end{array} \right..\)
Chọn C.