Phương pháp giải:

Công thức tính cường độ âm tại điểm cách nguồn P một đoạn R là: \(I=\frac{P}{4\pi {{R}^{2}}}\)

Mức cường độ âm: \(L=10\lg \frac{I}{{{I}_{0}}}(dB)\)  với I₀ = 10^-12W/m²

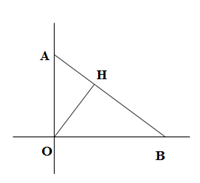
Tam giác OAB vuông tại O có đường cao OH thì:

\(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}\)

Lời giải chi tiết:

Cường độ âm tại A là:

\({{I}_{A}}=\frac{P}{4\pi .O{{A}^{2}}}={{10}^{-12}}{{.10}^{4}}={{10}^{-8}}\text{W}/{{m}^{2}}\Rightarrow \frac{1}{O{{A}^{2}}}=\frac{4\pi {{.10}^{-8}}}{P}\)      (1)

Máy thu di chuyển trên đường thẳng AB tới nơi có cường độ âm lớn nhất thì khoảng cách từ máy thu đến nguồn nhỏ nhất, vậy khi đó máy thu nằm ở H là đường cao hạ từ O đến AB.

Cường độ âm tại H khi đó :

            \({{I}_{H}}=\frac{P+63P}{4\pi .O{{H}^{2}}}=\frac{64P}{4\pi .O{{H}^{2}}}={{10}^{-12}}{{.10}^{6}}={{10}^{-6}}\text{W}/{{m}^{2}}\Rightarrow \frac{1}{O{{H}^{2}}}=\frac{4\pi {{.10}^{-6}}}{64P}\)(2)

Từ (1) và (2) ta được : \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}\Rightarrow \frac{1}{O{{B}^{2}}}=\frac{1}{O{{H}^{2}}}-\frac{1}{O{{A}^{2}}}=\frac{4\pi {{.10}^{-6}}}{64P}-\frac{4\pi {{.10}^{-8}}}{P}\)

Khi công suất là P thì cường độ âm tại B là :

            \({{I}_{B}}=\frac{P}{4\pi .O{{B}^{2}}}=\frac{P}{4\pi }.\left( \frac{4\pi {{.10}^{-6}}}{64P}-\frac{4\pi {{.10}^{-8}}}{P} \right)={{5,625.10}^{-9}}\text{W}/{{m}^{2}}\)

Vậy mức cường độ âm tại B là : \({{L}_{B}}=10\lg \frac{{{I}_{B}}}{{{I}_{0}}}=37,5(dB)\)