Câu hỏi
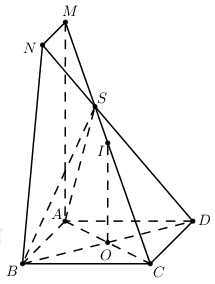
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2 Biết rằng \(\widehat {ASB} = \widehat {ASD} = {90^0}\), mặt phẳng chứa AB và vuông góc với (ABCD) cắt SD tại N. Tìm giá trị lớn nhất của thể tích tứ diện DABN.
- A \(\dfrac{{2{a^3}}}{3}\)
- B \(\dfrac{{2\sqrt 3 {a^3}}}{3}\)
- C \(\dfrac{{4{a^3}}}{3}\)
- D \(\dfrac{{4\sqrt 3 {a^3}}}{3}\)
Lời giải chi tiết:
Gọi \(O = AC \cap BD\) và \(\left( P \right)\) là mặt phẳng chứa AB và vuông góc với \(\left( {ABCD} \right)\).
Ta có \(\left\{ \begin{array}{l}SA \bot SB\\SA \bot SD\end{array} \right. \Rightarrow SA \bot \left( {SBD} \right) \Rightarrow SA \bot BD\)
Và \(\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)\).
Trong \(SAC\) kẻ đường thẳng \(OI \bot AC\,\,\left( {I \in SC} \right)\).
Ta có \(OI \subset \left( {SAC} \right) \Rightarrow OI \bot BD\), \(OI \bot AC \Rightarrow OI \bot \left( {ABCD} \right) \Rightarrow \left( P \right)//\left( {OI} \right)\).
Trong \(\left( {SAC} \right)\) kẻ \(AM//OI\,\,\left( {M \in SC} \right)\).
\(\left( P \right)\) và \(\left( {SCD} \right)\) có điểm M chung, \(AB//CD \Rightarrow \left( P \right) \cap \left( {SCD} \right)\)= đường thẳng qua M và song song với AB, CD.
Trong \(\left( {SCD} \right)\) kẻ \(MN//CD\,\,\left( {N \in SD} \right)\). Khi đó \(\left( P \right) \equiv \left( {ABMN} \right)\).
Ta có \({V_{D.ABN}} = \dfrac{1}{3}{S_{\Delta ABD}}.d\left( {N;\left( {ABD} \right)} \right) = \dfrac{1}{3}{S_{\Delta ABD}}.d\left( {M;\left( {ABD} \right)} \right) = \dfrac{2}{3}{S_{\Delta ABD}}.d\left( {I;\left( {ABD} \right)} \right) = \dfrac{2}{3}IO.{S_{\Delta ABD}}\)
\( \Rightarrow {V_{D.ABN}} = \dfrac{2}{3}IO.\dfrac{1}{2}.4{a^2} = \dfrac{{4{a^2}}}{3}IO\).
Do đó để \({V_{D.ABN}}\) lớn nhất thì \(OI\) phải lớn nhất.
Vì \(SA \bot \left( {SBD} \right)\,\,\left( {cmt} \right) \Rightarrow SA \bot SO \Rightarrow \Delta SOA\) vuông tại S.
Đặt \(SA = x\,\,\left( {0 < x < a\sqrt 2 = OA} \right)\). Ta có \(OA = \dfrac{1}{2}AC = \dfrac{1}{2}.2a\sqrt 2 = a\sqrt 2 \Rightarrow SO = \sqrt {O{A^2} - S{A^2}} = \sqrt {2{a^2} - {x^2}} \).
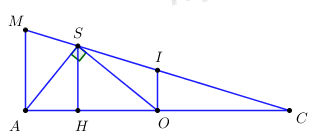
Kẻ \(SH \bot AC\,\,\left( {H \in AC} \right)\) ta có \(SH = \dfrac{{SA.SO}}{{\sqrt {S{A^2} + S{O^2}} }} = \dfrac{{x.\sqrt {2{a^2} - {x^2}} }}{{\sqrt {{x^2} + 2{a^2} - {x^2}} }} = \dfrac{{x\sqrt {2{a^2} - {x^2}} }}{{a\sqrt 2 }}\); \(OH = \dfrac{{S{O^2}}}{{OA}} = \dfrac{{2{a^2} - {x^2}}}{{a\sqrt 2 }}\).
\(CH = OC + OH = a\sqrt 2 + \dfrac{{2{a^2} - {x^2}}}{{a\sqrt 2 }} = \dfrac{{4{a^2} - {x^2}}}{{a\sqrt 2 }}\)
Áp dụng định lí Ta-lét (OI // SH) ta có:
\(\dfrac{{OI}}{{SH}} = \dfrac{{OC}}{{CH}} \Rightarrow OI = \dfrac{{\dfrac{{x\sqrt {2{a^2} - {x^2}} }}{{a\sqrt 2 }}.a\sqrt 2 }}{{\dfrac{{4{a^2} - {x^2}}}{{a\sqrt 2 }}}} = \dfrac{{x\sqrt {2{a^2} - {x^2}} .a\sqrt 2 }}{{4{a^2} - {x^2}}} = a\dfrac{{x\sqrt {4{a^2} - 2{x^2}} }}{{4{a^2} - {x^2}}}\)
Áp dụng BĐT Cô-si cho hai số không âm\(x\) và \(\sqrt {4{a^2} - 2{x^2}} \) ta có: \(x\sqrt {4{a^2} - 2{x^2}} \le \dfrac{{{x^2} + 4{a^2} - 2{x^2}}}{2} = \dfrac{{4{a^2} - {x^2}}}{2}\)
\( \Rightarrow OI \le a\dfrac{{\dfrac{{4{a^2} - {x^2}}}{2}}}{{4{a^2} - {x^2}}} = \dfrac{a}{2}\). Dấu "=" xảy ra \( \Leftrightarrow x = \sqrt {4{a^2} - 2{x^2}} \Leftrightarrow {x^2} = 4{a^2} - 2{x^2} \Leftrightarrow {x^2} = \dfrac{4}{3}{a^2} \Leftrightarrow x = \dfrac{{2a}}{{\sqrt 3 }}\).
Vậy \({V_{DABN}} \le \dfrac{{4{a^2}}}{3}.\dfrac{a}{2} = \dfrac{{2{a^3}}}{3}\) hay \(\max {V_{DABN}} = \dfrac{{2{a^3}}}{3}\).
Chọn A.