Câu hỏi
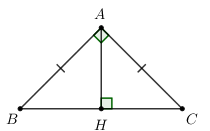
Cho tam giác ABC vuông cân tại A, đường cao \(AH = 4\). Tính diện tích xung quanh Sxq của hình nón nhận được khi quay tam giác ABC quanh trục AH.
- A \({S_{xq}} = 4\sqrt 2 \pi \)
- B \({S_{xq}} = 16\sqrt 2 \pi \)
- C \({S_{xq}} = 8\sqrt 2 \pi \)
- D \({S_{xq}} = 32\sqrt 2 \pi \)
Phương pháp giải:
Sử dụng công thức tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl\) trong đó r, l lần lượt là bán kính đáy và độ dài đường sinh của hình nón.
Lời giải chi tiết:
Khi quay tam giác vuông cân ABC quanh AH ta được khối nón có chiều cao \(AH = 4\), bán kính đáy \(BH = AH = 4\). Áp dụng định lí Pytago trong tam giác vuông ABH có \(AB = AH\sqrt 2 = 4\sqrt 2 \)
Khi đó diện tích xung quanh của hình nón là
\({S_{xq}} = \pi .AH.AB = \pi .4.4\sqrt 2 = 16\sqrt 2 \pi \).
Chọn B.
Câu hỏi trước
