Câu hỏi
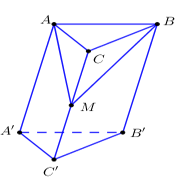
Cho khối lăng trụ tam giác ABA’B’C’ có thể tích V. Gọi M là trung điểm của CC’. Mặt phẳng (MAB) chia khối lăng trụ thành hai phần. Tính tỉ số thể tích hai phần đó (số bé chia số lớn).
- A \(\dfrac{2}{5}\)
- B \(\dfrac{3}{5}\)
- C \(\dfrac{1}{5}\)
- D \(\dfrac{1}{6}\)
Phương pháp giải:
So sánh tỉ số diện tích đáy và tỉ số chiều cao, từ đó suy ra tỉ số thể tích.
Lời giải chi tiết:
Ta có \(\dfrac{{{V_{M.ABC}}}}{{{V_{ABC.A'B'C'}}}} = \dfrac{{\dfrac{1}{3}.d\left( {M;\left( {ABC} \right)} \right).{S_{\Delta ABC}}}}{{d\left( {C';\left( {ABC} \right)} \right).{S_{\Delta ABC}}}} = \dfrac{1}{3}.\dfrac{1}{2} = \dfrac{1}{6}\)
Do đó tỉ số thể tích hai phần (số bé chia số lớn) mà mặt phẳng (MAB) chia ra là \(\dfrac{1}{5}\).
Chọn C.
Câu hỏi trước
