Phương pháp giải:

+) Xác định điểm Q dựa vào các yếu tố song song.

+) Gọi V₁ là thể tích của khối MAQNCP và V₂ là thể tích của khối còn lại, ta có: \({V_2} = {V_{M.BNP}} + {V_{Q.BPD}} + {V_{P.BMQ}}\)

+) So sánh tỉ số diện tích đáy và chiều cao, tính thể tích các khối thành phần của V₂, tính V₂, từ đó tính V₁.

Lời giải chi tiết:

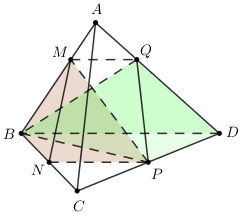
\(\left( {MNP} \right)\) và \(\left( {ABD} \right)\) có điểm M chung, \(\left\{ \begin{array}{l}NP \subset \left( {MNP} \right)\\BD \subset \left( {ABD} \right)\end{array} \right.\), NP // BD (do NP là đường trung bình của tam giác BCD), do đó giao tuyến của \(\left( {MNP} \right)\) và \(\left( {ABD} \right)\) là đường thẳng qua M và song song với NP, BD.

Trong (ABD) qua M kẻ \(MQ//BD\,\,\left( {Q \in AD} \right)\).

Gọi V₁ là thể tích của khối MAQNCP và V₂ là thể tích của khối còn lại, ta có:

\({V_2} = {V_{M.BNP}} + {V_{Q.BPD}} + {V_{P.BMQ}}\)

Ta có

 \(\begin{array}{l}\dfrac{{{S_{BNP}}}}{{{S_{BCD}}}} = \dfrac{{\dfrac{1}{2}d\left( {B;NP} \right).NP}}{{\dfrac{1}{2}d\left( {C;BD} \right).BD}} = \dfrac{{BN}}{{BC}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4}\\\dfrac{{d\left( {M;\left( {BNP} \right)} \right)}}{{d\left( {A;\left( {BCD} \right)} \right)}} = \dfrac{{MB}}{{AB}} = \dfrac{2}{3}\\ \Rightarrow \dfrac{{{V_{M.BNP}}}}{{{V_{A.BCD}}}} = \dfrac{1}{4}.\dfrac{2}{3} = \dfrac{1}{6} \Rightarrow {V_{M.BNP}} = \dfrac{1}{6}\end{array}\)

Tương tự ta có: \(\dfrac{{{S_{Q.BPD}}}}{{{V_{A.BCD}}}} = \dfrac{1}{2}.\dfrac{2}{3} = \dfrac{1}{3} \Rightarrow {S_{Q.BPD}} = \dfrac{1}{3}\).

\(\begin{array}{l}\dfrac{{{S_{BMQ}}}}{{{S_{ABD}}}} = \dfrac{{\dfrac{1}{2}d\left( {B;MQ} \right).MQ}}{{\dfrac{1}{2}d\left( {A;BD} \right).BD}} = \dfrac{{MB}}{{AB}}.\dfrac{{MQ}}{{BD}} = \dfrac{2}{3}.\dfrac{1}{3} = \dfrac{2}{9}\\\dfrac{{d\left( {P;\left( {BMQ} \right)} \right)}}{{d\left( {C;\left( {ABD} \right)} \right)}} = \dfrac{{PD}}{{CD}} = \dfrac{1}{2}\\ \Rightarrow \dfrac{{{V_{P.BMQ}}}}{{{V_{ABCD}}}} = \dfrac{2}{9}.\dfrac{1}{2} = \dfrac{1}{9} \Rightarrow {V_{P.BMQ}} = \dfrac{1}{9}\end{array}\)

\( \Rightarrow {V_2} = {V_{M.BNP}} + {V_{Q.BPD}} + {V_{P.BMQ}} = \dfrac{1}{6} + \dfrac{1}{3} + \dfrac{1}{9} = \dfrac{{11}}{{18}}\).

Vậy \({V_1} = 1 - {V_2} = 1 - \dfrac{{11}}{{18}} = \dfrac{7}{{18}}\).

Chọn C.