Lời giải chi tiết:

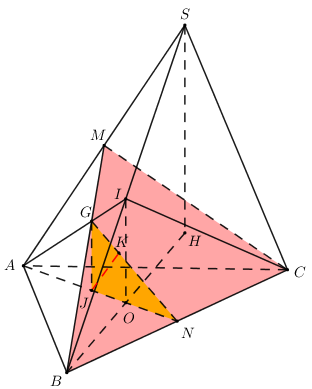
Gọi I là trung điểm của SB ta có:

Tam giác vuông tại A nên \(IA = IS = IB\),  vuông tại C nên \(IC = IS = IB\).

Do đó \(IA = IB = IC\). Gọi O là tâm tam giác đều ABC \( \Rightarrow IO \bot \left( {ABC} \right)\).

Trong mặt phẳng tạo bởi SB và BO kẻ \(SH//IO\,\,\left( {H \in BO} \right) \Rightarrow SH \bot \left( {ABC} \right)\).

Gọi N là trung điểm của BC, \(G = AI \cap BM \Rightarrow \) G là trọng tâm tam giác SAB, trong (AGN) dựng \(GJ//IO\,\,\left( {J \in AN} \right) \Rightarrow GJ \bot \left( {ABCD} \right)\).

Trong (GJN) kẻ \(JK \bot GN\,\,\left( {K \in GN} \right)\). Ta có : \(\left\{ \begin{array}{l}BC \bot GJ\\BC \bot JN\end{array} \right. \Rightarrow BC \bot \left( {GJN} \right) \Rightarrow BC \bot JK \Rightarrow JK \bot \left( {MBC} \right) \Rightarrow JK = d\left( {J;\left( {MBC} \right)} \right)\)

Ta có : \(\begin{array}{l}AJ \cap \left( {BMC} \right) = N \Rightarrow \frac{{d\left( {A;\left( {MBC} \right)} \right)}}{{d\left( {J;MBC} \right)}} = \frac{{AN}}{{JN}} = \frac{{AN}}{{AN - AJ}}\\AN = \frac{{2a\sqrt 3 }}{2} = a\sqrt 3\end{array}\)

Áp dụng định lí Ta-lét ta có : \(\begin{array}{l}\frac{{AJ}}{{AO}} = \frac{{AG}}{{AI}} = \frac{2}{3} \Rightarrow AJ = \frac{2}{3}AO = \frac{2}{3}.\frac{2}{3}AN = \frac{4}{9}.\frac{{2a\sqrt 3 }}{2} = \frac{{4a\sqrt 3 }}{9}\\ \Rightarrow \frac{{d\left( {A;\left( {MBC} \right)} \right)}}{{d\left( {J;\left( {MBC} \right)} \right)}} = \frac{{a\sqrt 3 }}{{a\sqrt 3  - \frac{{4a\sqrt 3 }}{9}}} = \frac{9}{5} \Leftrightarrow d\left( {J;\left( {MBC} \right)} \right) = \frac{{5d\left( {A;\left( {MBC} \right)} \right)}}{9} = \frac{{10\sqrt {21} a}}{{63}}\end{array}\).

Ta có \(JN = AN - AJ = a\sqrt 3  - \frac{{4a\sqrt 3 }}{9} = \frac{{5a\sqrt 3 }}{9}\).

Áp dụng hệ thức lượng trong tam giác vuông GJN ta có :

\(\begin{array}{l}\frac{1}{{J{K^2}}} = \frac{1}{{J{G^2}}} + \frac{1}{{J{N^2}}} \Leftrightarrow \frac{1}{{J{G^2}}} = \frac{1}{{J{K^2}}} - \frac{1}{{J{N^2}}}\\\,\,\,\,\,\,\,\,\,\, = \frac{1}{{{{\left( {\frac{{10\sqrt {21} a}}{{63}}} \right)}^2}}} - \frac{1}{{{{\left( {\frac{{5a\sqrt 3 }}{9}} \right)}^2}}} = \frac{{189}}{{100{a^2}}} - \frac{{27}}{{25{a^2}}} = \frac{{81}}{{100{a^2}}} \Leftrightarrow IG = \frac{{10a}}{9}\end{array}\).

Ta có \(\begin{array}{l}\frac{{JG}}{{IO}} = \frac{{AG}}{{AI}} = \frac{2}{3} \Rightarrow IO = \frac{3}{2}JG\\SH = 2IO \Rightarrow SH = 3JG = \frac{{10a}}{3}\\ \Rightarrow {V_{S.ABC}} = \frac{1}{3}.SH.{S_{\Delta ABC}} = \frac{1}{3}.\frac{{10a}}{3}.\frac{{{{\left( {2a} \right)}^2}\sqrt 3 }}{4} = \frac{{10\sqrt 3 {a^3}}}{9}\end{array}\)

Chọn A.