Phương pháp giải:

+) Tính y’. Hàm số đồng biến trên \(\left( {0; + \infty } \right) \Leftrightarrow y' \ge 0\,\,\forall x \in \left( {0; + \infty } \right)\) và bằng 0 tại hữu hạn điểm.

+) Cô lập m, đưa bất phương trình về dạng \(m \le f\left( x \right)\,\,\forall x \in \left( {0; + \infty } \right) \Leftrightarrow m \le \mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right).\).

+) Xét hàm số \(y = f\left( x \right)\) trên \(\left( {0; + \infty } \right)\), lập BBT tìm \(\mathop {\min }\limits_{\left( {0; + \infty } \right)} f\left( x \right)\)  

Lời giải chi tiết:

TXĐ: \(D = R\backslash \left\{ 0 \right\}\). Ta có \(y' = 3{x^2} + m - \frac{3}{{28}}\left( { - 2\frac{1}{{{x^3}}}} \right) = 3{x^2} + m + \frac{3}{{14{x^3}}}\).

Để hàm số đồng biến trên khoảng \(\left( {0; + \infty } \right)\) thì \(y' \ge 0\,\,\forall x \in \left( {0; + \infty } \right)\) và bằng 0 tại hữu hạn điểm.

\(\begin{array}{l} \Leftrightarrow 3{x^2} + m + \frac{3}{{14{x^3}}} \ge 0\,\,\forall x \in \left( {0; + \infty } \right)\\ \Leftrightarrow 3{x^2} + \frac{3}{{14{x^3}}} \ge  - m\,\,\forall x \in \left( {0; + \infty } \right)\end{array}\)  

Đặt \(f\left( x \right) = 3{x^2} + \frac{3}{{14{x^3}}} \Rightarrow f\left( x \right) \ge  - m\,\,\forall x \in \left( {0; + \infty } \right) \Leftrightarrow  - m \le \mathop {\min }\limits_{\left[ {0; + \infty } \right)} f\left( x \right)\).

Xét hàm số \(f\left( x \right) = 3{x^2} + \frac{3}{{14{x^3}}}\) trên \(\left( {0; + \infty } \right)\) ta có:

\(f'\left( x \right) = 6x + \frac{3}{{35}}.\left( { - \frac{3}{{{x^4}}}} \right) = 6x - \frac{9}{{14{x^4}}} = 0 \Leftrightarrow 6x = \frac{9}{{14{x^4}}} \Leftrightarrow {x^5} = \frac{3}{{28}} \Leftrightarrow x = \sqrt[5]{{\frac{3}{{28}}}}\).

BBT:

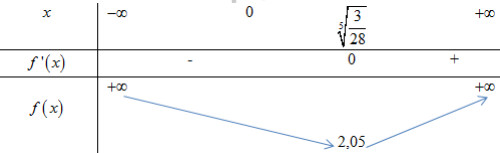
\(\Rightarrow  - m \le 2,05 \Leftrightarrow m \ge  - 2,05\). Mà m là số nguyên âm \(\Rightarrow m \in \left\{ { - 2; - 1} \right\}\). Vậy tổng các giá trị của m thỏa mãn yêu cầu bài toán là -2 – 1 = -3.

Chọn C.