Câu hỏi
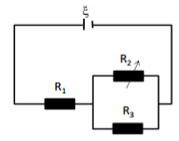
Cho mạch điện như hình vẽ. Nguồn điện có điện trở trong bằng \(2\,\,\Omega ;{R_1} = 8\,\,\Omega ;{R_3} = 15\,\,\Omega \). Tính \({R_2}\) để công suất tiêu thụ trên \({R_2}\) đạt cực đại.
- A \(2\,\,\Omega \)
- B \(10\,\,\Omega \)
- C \(6\,\,\Omega \)
- D \(25\,\,\Omega \)
Phương pháp giải:
Định luật Ôm cho toàn mạch: \(I = \frac{E}{{R + r}}\)
Áp dụng bất đẳng thức Cô - si
Lời giải chi tiết:
Cường độ dòng điện chạy trong mạch chính là:
\(I = {E \over {{R_N} + r}} = {E \over {10 + {{15{R_2}} \over {15 + {R_2}}}}} = {{\left( {{R_2} + 15} \right)E} \over {25{R_2} + 150}}\)
Cường độ dòng điện chạy qua \({R_2}\) là:
\({I_2} = I.{{{R_{23}}} \over {{R_2}}} = {{E\left( {{R_2} + 15} \right)} \over {25{R_2} + 150}}.{{15{R_2}} \over {{R_2} + 15}}.{1 \over {{R_2}}} = {{15E} \over {25{R_2} + 150}}\)
Công suất tiêu thụ trên \({R_2}\) là:
\(P = I_2^2{R_2} = {\left( {{{15E} \over {25{R_2} + 150}}} \right)^2}.{R_2} = {{225{E^2}} \over {{{\left( {25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }}} \right)}^2}}}\)
Để \({P_{\max }}\) thì \(25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }}\) phải nhỏ nhất
Theo bất đẳng thức Cô - si ta có:
\(25\sqrt {{R_2}} + {{150} \over {\sqrt {{R_2}} }} \ge 2\sqrt {25\sqrt {{R_2}} .{{150} \over {\sqrt {{R_2}} }}} = 50\sqrt 6 \)
Dấu “=” xảy ra khi \(25\sqrt {{R_2}} = {{150} \over {\sqrt {{R_2}} }} \Leftrightarrow {R_2} = {{150} \over {25}} = 6\Omega \)
Chọn C.