Câu hỏi
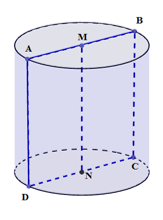
Cho hình chữ nhật \(ABCD\) có \(AB = 2AD\) và \(M,N\) lần lượt là trung điểm của các cạnh \(AB,CD\). Khi quay hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) ta được một khối tròn xoay có thể tích bằng \(8\pi {a^3}\). Diện tích hình chữ nhật \(ABCD\)là
- A \(2{a^2}\).
- B \(16{a^2}\).
- C \(8{a^2}\).
- D \(4{a^2}\).
Phương pháp giải:
+) Đặt độ dài \(AD = x \Rightarrow AB = 2x\).
+) Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\).
+) Tính iện tích hình chữ nhật \(ABCD\): \({S_{ABCD}} = AD.AB\).
Lời giải chi tiết:
Đặt độ dài \(AD = x \Rightarrow AB = 2x\).
Khi quay hình chữ nhật \(ABCD\) quanh đường thẳng \(MN\) ta được một khối trụ có đường cao \(h = AD = x\), bán kính đáy \(r = MA = \dfrac{{AB}}{2} = x\), có thể tích là:
\(V = \pi {r^2}h = \pi .{x^2}.x = \pi {x^3} \Rightarrow \pi {x^3} = 8\pi {a^3} \Leftrightarrow x = 2a \Rightarrow \left\{ \begin{array}{l}AD = 2a\\AB = 4a\end{array} \right..\)
Diện tích hình chữ nhật \(ABCD\)là: \(AD.AB = 2a.4a = 8{a^2}\).
Chọn: C







