Câu hỏi
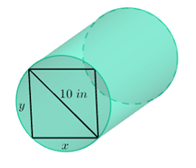
Một lĩnh vực xây dựng, độ bền d của một thanh xà bằng gỗ có dạng một khối trụ (được cắt ra từ một khúc gỗ, với các kích thước như hình bên dưới; biết 1 in bằng 2,54cm) được tính theo công thức \(d = 13,8x{y^2}\). Giá trị gần đúng của x sao cho thanh xà có độ bền cao nhất là:
- A \(4,81\,in\).
- B \(8,33\,\,in\).
- C \(5,77\,in\).
- D \(3,33\,in\).
Phương pháp giải:
Sử dụng phương pháp hàm số để giải bài toán.
Lời giải chi tiết:
Ta có: \({x^2} + {y^2} = {10^2} \Leftrightarrow {y^2} = 100 - {x^2}\)
Khi đó, \(d = 13,8x{y^2} = 13,8x\left( {100 - {x^2}} \right) = 13,8\left( {100x - {x^3}} \right)\)
Xét hàm số \(f\left( x \right) = 13,8\left( {100x - {x^3}} \right),\,\,x \in \left( {0;10} \right)\,\, \Rightarrow y' = 13,8\left( {100 - 3{x^2}} \right);\,\,y' = 0 \Leftrightarrow x = \dfrac{{10}}{{\sqrt 3 }}\)
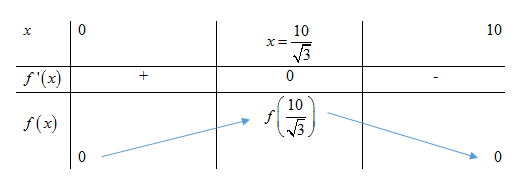
\( \Rightarrow \mathop {\max }\limits_{\left( {0;10} \right)} f\left( x \right) = f\left( {\dfrac{{10}}{{\sqrt 3 }}} \right)\)
Vậy để thanh xà có độ bên cao nhất thì \(x = \dfrac{{10}}{{\sqrt 3 }} \approx 5,77\) (in)
Chọn: C







