Phương pháp giải:

+) Xác định các điểm cực trị của đồ thị hàm số.

+) Tính giá trị của biểu thức.

Lời giải chi tiết:

TXĐ: \(D = R{\rm{\backslash }}\left\{ { - 2} \right\}\)

\(y = \dfrac{{{x^2} + 3x + 3}}{{x + 2}} \Rightarrow y' = \dfrac{{\left( {2x + 3} \right)\left( {x + 2} \right) - \left( {{x^2} + 3x + 3} \right)}}{{{{\left( {x + 2} \right)}^2}}} = \dfrac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}}\)

\(y' = 0 \Leftrightarrow \dfrac{{{x^2} + 4x + 3}}{{{{\left( {x + 2} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x =  - 1\\x =  - 3\end{array} \right.\)

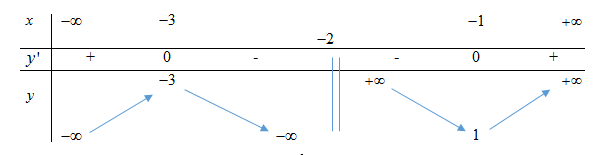
Hàm số đã cho có giá trị cực đại và giá trị cực tiểu lần lượt là \({y_{CD}} =  - 3,\,\,{y_{CT}} = 1 \Rightarrow \)\(y_{CD}^2 - 2\,\,y_{CT}^2 = 7\).

Chọn: D