Câu hỏi
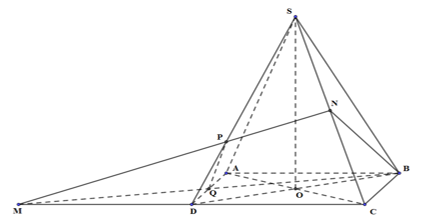
Cho khối chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(a\), góc giữa cạnh bên và mặt đáy bằng \(60^\circ \). Gọi \(M\) là điểm đối xứng với \(C\) qua \(D\) và \(N\) là trung điểm của cạnh \(SC\). Mặt phẳng \((BMN)\) chia khối chóp \(S.ABCD\) thành hai khối đa diện \(\left( {{H_1}} \right)\) và \(\left( {{H_2}} \right)\), trong đó \(\left( {{H_1}} \right)\) chứa điểm \(C\). Thể tích của khối \(\left( {{H_1}} \right)\) là:
- A \(\dfrac{{7\sqrt 6 {a^3}}}{{72}}\).
- B \(\dfrac{{5\sqrt 6 {a^3}}}{{72}}\).
- C \(\dfrac{{7\sqrt 6 {a^3}}}{{36}}\).
- D \(\dfrac{{5\sqrt 6 {a^3}}}{{36}}\).
Phương pháp giải:
Sử dụng công thức tỉ số thể tích cho khối chóp tam giác
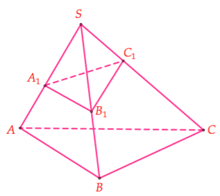
(Công thức Simson): Cho khối chóp S.ABC, các điểm \({A_1},\,{B_1},\,{C_1}\) lần lượt thuộc \(SA,\,SB,\,SC\). Khi đó,
\(\dfrac{{{V_{S.\,{A_1}{B_1}{C_1}}}}}{{{V_{S.ABC}}}} = \dfrac{{S{A_1}}}{{SA}}.\dfrac{{S{B_1}}}{{SB}}.\dfrac{{S{C_1}}}{{SC}}\)
Lời giải chi tiết:
Trong (SCD), gọi \(P = MN \cap SD\) ; trong (ABCD), gọi \(Q = MB \cap AD\)
\( \Rightarrow \) Thiết diện của khối chóp cắt bởi (MNB) là tứ giác BNPQ.
ABCD là hình vuông cạnh a \( \Rightarrow OA = \dfrac{{AD}}{{\sqrt 2 }} = \dfrac{a}{{\sqrt 2 }}\)
S.ABCD là chóp tứ giác đều \( \Rightarrow SO \bot \left( {ABCD} \right) \Rightarrow \left( {\widehat {SA;\left( {ABCD} \right)}} \right) = \left( {\widehat {SA;AO}} \right) = \widehat {SAO} = 60^\circ \)
\(\Delta \)SAO vuông tại O \( \Rightarrow SO = OA.\tan \widehat {SAO} = \dfrac{a}{{\sqrt 2 }}.\tan 60^\circ = \dfrac{{a\sqrt 6 }}{2}\)
\(\Delta \)SMC có: MN, SD là trung tuyến, \(MN \cap SD = P \Rightarrow P\) là trọng tâm \(\Delta \)SMC \( \Rightarrow \dfrac{{MP}}{{MN}} = \dfrac{2}{3}\)
Do \(\Delta MDQ = \Delta BAQ\,(g.c.g) \Rightarrow MQ = QB\)
Ta có:
\(\dfrac{{{V_{M.PDQ}}}}{{{V_{M.NCB}}}} = \dfrac{{MD}}{{MC}}.\dfrac{{MP}}{{MN}}.\dfrac{{MQ}}{{MB}} = \dfrac{1}{2}.\dfrac{2}{3}.\dfrac{1}{2} = \dfrac{1}{6} \Rightarrow {V_{M.PDQ}} = \dfrac{1}{6}{V_{M.NCB}} \Rightarrow {V_{CDQBNP}} = \dfrac{5}{6}{V_{M.NCB}}\)
\( \Leftrightarrow {V_{{H_1}}} = \dfrac{5}{6}{V_{M.NCB}}\)
Ta lại có:
\({V_{M.NCB}} = \dfrac{1}{3}.{d_{\left( {N;\left( {ABCD} \right)} \right)}}.{S_{\Delta MBC}} = \dfrac{1}{3}.\dfrac{1}{2}{d_{\left( {S;\left( {ABCD} \right)} \right)}}.\left( {\dfrac{1}{2}.MC.BC} \right) = \dfrac{1}{3}.\dfrac{1}{2}.SO.\left( {DC.BC} \right)\)\( = \dfrac{1}{3}.\dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{2}.a.a = \dfrac{{{a^3}\sqrt 6 }}{{12}}\)
\( \Rightarrow {V_{{H_1}}} = \dfrac{5}{6}.\dfrac{{{a^3}\sqrt 6 }}{{12}} = \dfrac{{5{a^3}\sqrt 6 }}{{72}}\).
Chọn: B