Câu hỏi
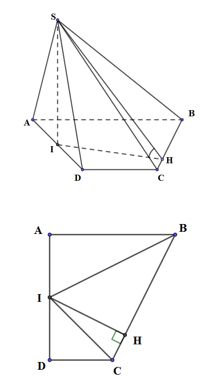
Cho khối chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D; AB = AD = 2a;CD = a . Góc giữa hai mặt phẳng (SBC) và (ABCD) bằng 600 . Gọi I là trung điểm của AD. Biết 2 mặt phẳng (SBI) và (SCI) cùng vuông góc với mặt phẳng (ABCD). Tính thể tích khối chóp S.ABCD.
- A \({V_{S.ABCD}} = 6{a^3}\sqrt 3 \)
- B \({V_{S.ABCD}} = \dfrac{{6{a^3}\sqrt {15} }}{5}\)
- C \({V_{S.ABCD}} = \dfrac{{3{a^3}\sqrt {15} }}{5}\)
- D \({V_{S.ABCD}} = 6{a^3}\)
Phương pháp giải:
\(\left\{ \begin{array}{l}\left( \alpha \right) \bot \left( \gamma \right)\\\left( \beta \right) \bot \left( \gamma \right)\\\left( \alpha \right) \cap \left( \beta \right) = d\end{array} \right. \Rightarrow d \bot \left( \gamma \right)\)
Lời giải chi tiết:
ABCD là hình thang vuông
\( \Rightarrow {S_{ABCD}} = \dfrac{1}{2}\left( {DC + AB} \right).AD = \dfrac{1}{2}.\left( {a + 2a} \right).2a = 3{a^2}\)
Kẻ IH vuông góc BC, (\(H \in BC\))
Ta có: \(\left\{ \begin{array}{l}\left( {SIB} \right) \bot \left( {ABCD} \right)\\\left( {SIC} \right) \bot \left( {ABCD} \right)\\\left( {SIB} \right) \cap \left( {SIC} \right) = SI\end{array} \right. \Rightarrow SI \bot \left( {ABCD} \right)\)
\( \Rightarrow SI \bot BC\), mà \(IH \bot BC \Rightarrow BC \bot \left( {SHI} \right)\)
\(\begin{array}{l}\left( {SBC} \right) \cap \left( {ABCD} \right) = BC\,\,\\ \Rightarrow \left( {\widehat {\left( {SBC} \right);\left( {ABCD} \right)}} \right) = \left( {\widehat {SH;IH}} \right) = \widehat {SHI} = 60^\circ \end{array}\)
*) Tính IH:
Ta có: \({S_{ABCD}} = 3{a^2}\), \({S_{\Delta ABI}} = {a^2},\,\,{S_{\Delta IDC}} = \dfrac{1}{2}{a^2}\)
\( \Rightarrow {S_{\Delta IBC}} = 3{a^2} - {a^2} - \dfrac{1}{2}{a^2} = \dfrac{3}{2}{a^2}\)
\(BC = \sqrt {{a^2} + {{\left( {2a} \right)}^2}} = \sqrt 5 a\)
\({S_{\Delta IBC}} = \dfrac{1}{2}.IH.BC \Rightarrow \dfrac{3}{2}{a^2} = \dfrac{1}{2}.IH.a\sqrt 5 \Rightarrow IH = \dfrac{{3a}}{{\sqrt 5 }}\)
Tam giác SIH vuông tại I
\( \Rightarrow SI = \tan 60^\circ .IH = \sqrt 3 .\dfrac{{3a}}{{\sqrt 5 }} = \dfrac{{3a\sqrt {15} }}{5}\)
*) Thể tích khối chóp S.ABCD:
\({V_{S.ABCD}} = \dfrac{1}{3}.SI.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{3a\sqrt {15} }}{5}.3{a^2} = \dfrac{{3{a^3}\sqrt {15} }}{5}\)
Chọn: C







