Câu hỏi
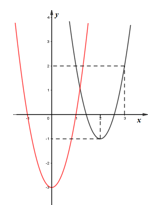
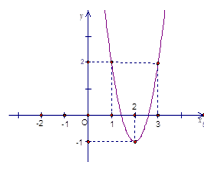
Cho hàm số \(y = f(x)\), biết rằng hàm số \(y = f'(x - 2) + 2\) có đồ thị như hình vẽ bên. Hỏi hàm số \(y = f(x)\) nghịch biến trên khoảng nào trong các khoảng dưới đây?
- A \(( - \infty ;2).\)
- B \(( - 1;1).\)
- C \((2; + \infty ).\)
- D \(\left( {\dfrac{3}{2};\dfrac{5}{2}} \right).\)
Phương pháp giải:
+) Từ đồ thị hàm số \(y = f'(x - 2) + 2\) ta dựng đồ thị hàm số \(y = f'(x)\) bằng cách: tịnh tiến đồ thị hàm số \(y = f'(x - 2) + 2\) sang trái 2 đơn vị và xuống dưới 2 đơn vị.
+) Quan sát đồ thị hàm số \(y = f'(x)\)) và xác định các khoảng của x làm cho \(f'\left( x \right) < 0\).
Lời giải chi tiết:
Từ đồ thị hàm số \(y = f'(x - 2) + 2\) ta dựng đồ thị hàm số \(y = f'(x)\) bằng cách: tịnh tiến đồ thị hàm số \(y = f'(x - 2) + 2\) sang trái 2 đơn vị và xuống dưới 2 đơn vị
Quan sát đồ thị hàm số \(y = f'(x)\) (đồ thị màu đỏ) ta có:
\(f'(x) < 0 \Leftrightarrow - 1 < x < 1\)
\( \Rightarrow \)Hàm số \(y = f(x)\) nghịch biến trên khoảng \(( - 1;1).\)
Chọn: B
Câu hỏi trước
