Câu hỏi
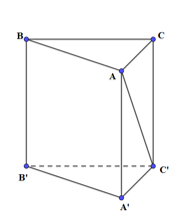
Cho hình lăng trụ đứng ABC.A’B’C’ có \(AB = a,\,AC = 2a,\widehat {BAC} = 120^\circ \), cạnh AC’ hợp với mặt đáy góc \(45^\circ \). Thể tích V của khối lăng trụ ABCA’B’C’ là:
- A \(V = \dfrac{{2{a^3}\sqrt 3 }}{3}\).
- B \(V = \dfrac{{{a^3}\sqrt 3 }}{3}\).
- C \(V = 2{a^3}\sqrt 3 \).
- D \(V = {a^3}\sqrt 3 \).
Phương pháp giải:
Thể tích khối lăng trụ: \(V = Sh\)
Lời giải chi tiết:
\(CC' \bot \left( {ABC} \right) \Rightarrow \widehat {\left( {AC';\left( {ABC} \right)} \right)} = \widehat {\left( {AC';AC} \right)} = \widehat {C'AC} = 45^\circ \)
\( \Rightarrow \Delta ACC'\) vuông cân tại C \( \Rightarrow CC' = AC = 2a\)
Diện tích tam giác ABC:
\({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat A = \dfrac{1}{2}.a.2a.\sin 120^\circ = \dfrac{1}{2}.a.2a.\dfrac{{\sqrt 3 }}{2} = \dfrac{{\sqrt 3 {a^2}}}{2}\)
Thể tích V của khối lăng trụ ABCA’B’C’ là: \(V = {S_{ABC}}.CC' = \dfrac{{{a^2}\sqrt 3 }}{2}.2a = {a^3}\sqrt 3 \).
Chọn: D
Câu hỏi trước
