Câu hỏi
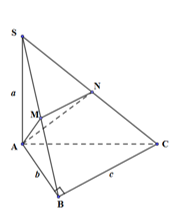
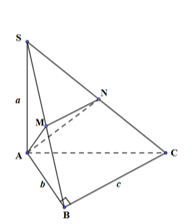
Cho hình vẽ bên với M, N lần lượt là trung điểm của các cạnh SB, SC. \(SA\) vuông góc với (ABC).
Thể tích V của khối đa diện ABCNM là:
- A \(V = \dfrac{1}{4}abc\).
- B \(V = \dfrac{1}{8}abc\).
- C \(V = \dfrac{1}{6}abc\).
- D \(V = \dfrac{1}{{24}}abc\).
Phương pháp giải:
\({V_{ABCNM}} = {V_{S.ABC}} - {V_{S.AMN}}\)
Lời giải chi tiết:
Ta có: \({V_{ABCNM}} = {V_{S.ABC}} - {V_{S.AMN}}\)
Mà \({V_{S.ABC}} = \dfrac{1}{3}.SA.{S_{ABC}} = \dfrac{1}{3}.a.\dfrac{1}{2}bc = \dfrac{1}{6}abc\)
\(\dfrac{{{V_{S.AMN}}}}{{{V_{S.ABC}}}} = \dfrac{{SM}}{{SB}}.\dfrac{{SN}}{{SC}} = \dfrac{1}{2}.\dfrac{1}{2} = \dfrac{1}{4} \Rightarrow {V_{S.AMN}} = \dfrac{{{V_{S.ABC}}}}{4} \Rightarrow {V_{ABCNM}} = {V_{S.ABC}} - {V_{S.AMN}} = \dfrac{3}{4}{V_{S.ABC}} = \dfrac{3}{4}.\dfrac{1}{6}abc = \dfrac{1}{8}abc\).
Chọn: B
Câu hỏi trước
