Câu hỏi
Cho hàm số \(y = (m - 1)x + m\).
Câu 1: Xác định giá trị của \(m\) để đồ thị của hàm số cắt trục tung tại điểm có tung độ bằng \(2\).
- A \(m = 1\)
- B \(m = 2\)
- C \(m = - 1\)
- D \(m = - 2\)
Phương pháp giải:
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng \(2 \Rightarrow A\left( {0;\;2} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm A vào công thức hàm số ta tìm được giá trị của m.
Lời giải chi tiết:
Đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\) nên đồ thị của hàm số đi qua điểm \(A(0\,;\,\,2)\)
\( \Leftrightarrow 2 = (m - 1).0 + m \Leftrightarrow m = 2\)
Vậy với \(m = 2\) thì đồ thị của hàm số cắt trục tung tại điểm của tung độ bằng \(2\).
Chọn B.
Câu 2: Xác định giá trị của \(m\) để đồ thị của hàm số cắt hoành tại điểm có hoành độ bằng \( - 3\).
- A \(m = \frac{1}{2}\)
- B \(m = \frac{3}{2}\)
- C \(m = \frac{5}{2}\)
- D \(m = \frac{2}{3}\)
Phương pháp giải:
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ bằng \( - 3 \Rightarrow B\left( { - 3;\;0} \right)\) thuộc đồ thị hàm số. Thay tọa độ điểm B vào công thức hàm số ta tìm được giá trị của m.
Lời giải chi tiết:
Đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( - 3\) nên đồ thị của hàm số đi qua điểm \(B( - 3\,;\,\,0)\)
\(\begin{array}{l} \Leftrightarrow 0 = (m - 1).( - 3) + m \Leftrightarrow 0 = - 3m + 3 + m\\ \Leftrightarrow 2m = 3 \Leftrightarrow m = \frac{3}{2}\end{array}\)
Vậy với \(m = \frac{3}{2}\) thì đồ thị của hàm số cắt trục hoành tại điểm của hoành độ bằng \( - 3\).
Chọn B.
Câu 3: Vẽ đồ thị của hai hàm số ứng với giá trị của \(m\) tìm được ở các câu 1) và 2) trên cùng hệ trục tọa độ \(Oxy\) và tìm tọa độ giao điểm của hai đường thẳng vừa vẽ được.
- A \(\left( {1;\,1} \right)\)
- B \(\left( {1;\, - 1} \right)\)
- C \(\left( { - 1;\,1} \right)\)
- D \(\left( { - 1;\, - 1} \right)\)
Phương pháp giải:
Lập bằng giá trị, vẽ đồ thị hàm số cả 2 đồ thị hàm số trên cùng hệ trục tọa độ.
+) Lập phương trình hoành độ giao điểm của hai đồ thị hàm số để tìm hoành độ giao điểm của hai đồ thị hàm số.
+) Thay hoành độ giao điểm vừa tìm được vào một trong hai công thức hàm số trên để tìm tung độ giao điểm của hai đồ thị.
Lời giải chi tiết:
+) Với \(m = 2\) hàm số trở thành \(y = x + 2\).
+) Với \(m = \frac{3}{2}\) hàm số trở thành \(y = \frac{1}{2}x + \frac{3}{2}\).
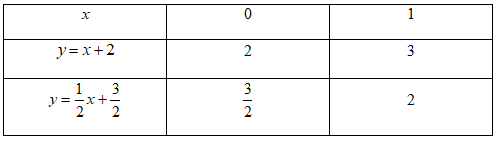
Ta có bảng giá trị:
Đồ thị của hàm số \(y = x + 2\) là đường thẳng đi qua hai điểm \((1\,;\,\,3)\) và \((0\,;\,\,2)\).
Đồ thị của hàm số \(y = \frac{1}{2}x + \frac{3}{2}\) là đường thẳng đi qua hai điểm \(\left( {0\,;\,\,\frac{3}{2}} \right)\) và \((1\,;\,\,2)\).
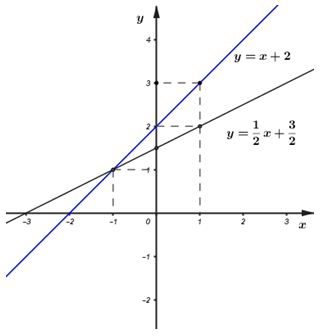
+) Vẽ đồ thị của hai hàm số:
+) Tìm tọa độ giao điểm của hai đồ thị hàm số.
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình:
\(\begin{array}{l}\;\;\;\;x + 2 = \frac{1}{2}x + \frac{3}{2} \Leftrightarrow x - \frac{1}{2}x = \frac{3}{2} - 2\\ \Leftrightarrow \frac{1}{2}x = \frac{{ - 1}}{2} \Leftrightarrow x = - 1\end{array}\)
Với \(x = - 1\) ta được \(y = - 1 + 2 = 1\).
Vậy tọa độ giao điểm của hai đường thẳng là \(( - 1\,;\,\,1)\).
Chọn C.