Câu hỏi
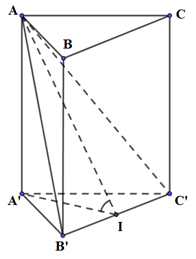
Cho khối lăng trụ đứng \(ABC.A'B'C'\) có đáy là tam giác cân \(ABC\) với \(AB = AC = a\), \(\widehat {BAC} = 120^\circ \), mặt phẳng \(\left( {AB'C'} \right)\) tạo với đáy một góc \(30^\circ \). Tính thể tích \(V\) của khối lăng trụ đã cho.
- A \(V = \frac{{{a^3}}}{6}\).
- B \(V = \frac{{{a^3}}}{8}\).
- C \(V = \frac{{{a^3}}}{8}\).
- D \(V = \frac{{9{a^3}}}{8}\).
Phương pháp giải:
Xác định góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\):
- Tìm giao tuyến \(\Delta \) của \(\left( \alpha \right),\,\,\left( \beta \right)\).
- Xác định 1 mặt phẳng \(\left( \gamma \right) \bot \Delta \).
- Tìm các giao tuyến \(a = \left( \alpha \right) \cap \left( \gamma \right),b = \left( \beta \right) \cap \left( \gamma \right)\)
- Góc giữa hai mặt phẳng \(\left( \alpha \right),\,\,\left( \beta \right)\): \(\widehat {\left( {\left( \alpha \right);\left( \beta \right)} \right)} = \widehat {\left( {a;b} \right)}\)
Lời giải chi tiết:
Mà \(AA' \bot B'C' \Rightarrow B'C' \bot \left( {AIA'} \right)\)
Ta có: \(\left\{ \begin{array}{l}\left( {AB'C'} \right) \cap \left( {A'B'C'} \right) = B'C'\\\left( {AIA'} \right) \bot B'C'\\\left( {AB'C'} \right) \cap \left( {AIA'} \right) = AI\\\left( {A'B'C'} \right) \cap \left( {AIA'} \right) = A'I\end{array} \right.\,\, \Rightarrow \widehat {\left( {\left( {AB'C'} \right);\left( {A'B'C'} \right)} \right)} = \widehat {AIA'} = 30^\circ \)
Gọi I là trung điểm của B’C’. Tam giác A’B’C’ cân tại A’ \( \Rightarrow A'I \bot B'C'\)
\(\Delta \)A’IB’ vuông tại I \( \Rightarrow A'I = A'B'.\sin \widehat {B'} = a.\sin 30^\circ = \frac{a}{2}\),
(\(\widehat {B'} = \widehat {C'} = \frac{{180^\circ - \widehat {A'}}}{2} = \frac{{180^\circ - 120^\circ }}{2} = 30^\circ \))
\(\Delta \)AIA’ vuông tại A’ \( \Rightarrow AA' = A'I.\tan \widehat {AIA'} = \frac{a}{2}.\tan 30^\circ = \frac{a}{{2\sqrt 3 }}\)
Diện tích tam giác ABC: \({S_{ABC}} = \frac{1}{2}.AB.AC.\sin \widehat A = \frac{1}{2}.a.a.\sin 120^\circ = \frac{{{a^2}\sqrt 3 }}{4}\)
Thể tích của khối lăng trụ đã cho là: \(V = AA'.{S_{ABC}} = \frac{a}{{2\sqrt 3 }}.\frac{{{a^2}\sqrt 3 }}{4} = \frac{{{a^3}}}{8}\).
Chọn: B