Phương pháp giải:

+) Gọi b là độ dài cạnh bên, sử dụng giả thiết diện tích xung quanh gấp đôi diện tích đáy biểu diễn b theo a.

+) Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

+) \({V_{S.ABCD}} = \dfrac{1}{3}SO.{S_{ABCD}}\).

Lời giải chi tiết:

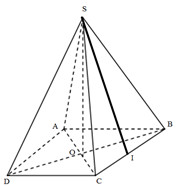
Gọi \(b\) là độ dài cạnh bên, I là trung điểm của BC\( \Rightarrow SI \bot BC\)

Tam giác \(SIB\) vuông tại I \( \Rightarrow SI = \sqrt {S{B^2} - I{B^2}}  = \sqrt {{b^2} - \dfrac{{{a^2}}}{4}} \)

\( \Rightarrow {S_{SBC}} = \dfrac{1}{2}.SI.BC = \dfrac{1}{2}.\sqrt {{b^2} - \dfrac{{{a^2}}}{4}} .a \Rightarrow {S_{xq}} = 4.{S_{SBC}} = 2a\sqrt {{b^2} - \dfrac{{{a^2}}}{4}} \)

Diện tích đáy: \({S_{ABCD}} = {a^2}\)

Theo đề bài, ta có: \(2a\sqrt {{b^2} - \dfrac{{{a^2}}}{4}}  = 2{a^2} \Leftrightarrow \sqrt {{b^2} - \dfrac{{{a^2}}}{4}}  = a \Leftrightarrow {b^2} - \dfrac{{{a^2}}}{4} = {a^2} \Leftrightarrow {b^2} = \dfrac{5}{4}{a^2} \Leftrightarrow b = \dfrac{{\sqrt 5 }}{2}a\)

ABCD là hình vuông cạnh a \( \Rightarrow OB = \dfrac{a}{{\sqrt 2 }}\).

Gọi \(O = AC \cap BD \Rightarrow SO \bot \left( {ABCD} \right)\).

Tam giác SOB vuông tại O \( \Rightarrow SO = \sqrt {S{B^2} - O{B^2}}  = \sqrt {\dfrac{5}{4}{a^2} - \dfrac{{{a^2}}}{2}}  = \dfrac{{\sqrt 3 }}{2}a\)

Thể tích của khối chóp : \({V_{S.ABCD}} = \dfrac{1}{3}.SO.{S_{ABCD}} = \dfrac{1}{3}.\dfrac{{\sqrt 3 }}{2}a.{a^2} = \dfrac{{\sqrt 3 {a^3}}}{6}\).

Chọn: D