Phương pháp giải:

+) Xác định m để phương trình hoành độ giao điểm có 3 nghiệm phân biệt.

+) Cô lập m, sử dụng phương pháp hàm số.

Lời giải chi tiết:

Phương trình hoành độ giao điểm của đồ thị hàm số \(y = {x^3} - mx + 1\) và trục hoành là: \({x^3} - mx + 1 = 0\)

\( \Leftrightarrow {x^3} - mx + 1 = 0 \Leftrightarrow mx = {x^3} + 1\) (*)

+) \(x = 0\) : (*) \( \Leftrightarrow m.0 = 1\): vô lý \( \Rightarrow \) Phương trình (*) không có nghiệm \(x = 0\) với mọi m

+) \(x \ne 0\): (*) \( \Leftrightarrow m = \dfrac{{{x^3} + 1}}{x} = {x^2} + \dfrac{1}{x}\,\,\left( {**} \right)\)

Xét hàm số \(f\left( x \right) = {x^2} + \dfrac{1}{x},\,\,\left( {x \ne 0} \right)\), \(f'\left( x \right) = 2x - \dfrac{1}{{{x^2}}} = \dfrac{{2{x^3} - 1}}{{{x^2}}}\), \(f'\left( x \right) = 0 \Leftrightarrow x = \dfrac{1}{{\sqrt[3]{2}}}\)

Bảng biến thiên:

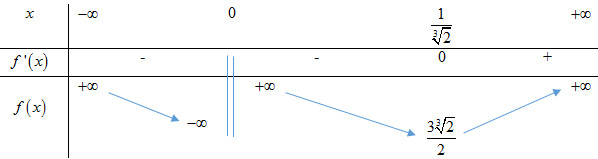
Số nghiệm của phương trình (**) là số giao điểm của đồ thị hàm số \(f\left( x \right) = {x^2} + \dfrac{1}{x}\) và đường thẳng \(y = m\) song song với trục hoành.

Để phương trình ban đầu có 3 nghiệm phân biệt \( \Leftrightarrow \left( {**} \right)\) có 3 nghiệm phân biệt khác 0 \( \Rightarrow m > \dfrac{{3\sqrt[3]{2}}}{2}\).

Chọn: B