Câu hỏi
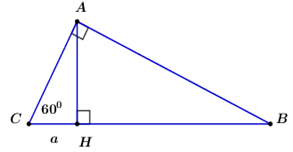
Cho tam giác \(ABC\) vuông tại \(A\) có đường cao \(AH\) (\(H\) thuộc \(BC\)). Biết \(\angle ACB = {60^0},\,\,CH = a\). Tính độ dài \(AB\) và \(AC\) theo \(a\).
- A \(\begin{array}{l}AB = 2\sqrt 3 a\\AC = 2a\end{array}\)
- B \(\begin{array}{l}AB = \sqrt 3 a\\AC = \frac{1}{2}a\end{array}\)
- C \(\begin{array}{l}AB = a\\AC = 3a\end{array}\)
- D \(\begin{array}{l}AB = \sqrt 3 a\\AC = a\end{array}\)
Phương pháp giải:
+) Sử dụng công thức lượng giác để tính các cạnh.
Lời giải chi tiết:
\(\Delta ACH\) vuông tại \(H\) có:
\(\cos C = \frac{{CH}}{{AC}}\,\,\, \Rightarrow AC = \frac{{CH}}{{\cos C}} = \frac{a}{{\cos {{60}^0}}} = \frac{a}{{\frac{1}{2}}} = 2a\)
\(\Delta ABC\) có \(AB = AC.\tan C = 2a.\tan {60^0} = 2\sqrt 3 a\)
Chọn D.
Câu hỏi trước
