Câu hỏi
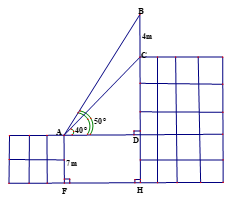
Trên nóc một toàn nhà có một cột ăg-ten thẳng cao 4m. Từ vị trí
quan sát A cao 7m so với mặt đất có thể nhìn thấy đỉnh B và chân
C của cột ăng-ten lần lượt dưới góc 500 và 400 so với phương nằm ngang (như hình vẽ bên)
Tính chiều cao CH của tòa nhà (kết quả làm tròn đến chữ số
thập phân thứ ba).
- A 16,518m
- B 17,318m
- C 15,718m
- D 11,518m
Lời giải chi tiết:
Xét tam giác ABD vuông tại D, ta có:
\(\tan BAD=\operatorname{t}\text{an}{{50}^{0}}=\frac{BD}{AD}=\frac{BC+CD}{AD}=\frac{4+CD}{AD}\Rightarrow AD=\frac{4+CD}{\tan {{50}^{0}}}\) (1)
Xét tam giác ACD vuông tại D, ta có:
\(\tan CAD=\operatorname{t}\text{an 4}{{0}^{0}}=\frac{CD}{AD}\Rightarrow AD=\frac{CD}{\tan {{40}^{0}}}\) (2)
Từ (1) và (2) \(\Rightarrow \frac{4+CD}{\tan {{50}^{0}}}=\frac{CD}{\tan {{40}^{0}}}\Leftrightarrow \tan {{40}^{0}}.\left( 4+CD \right)=\tan {{50}^{0}}.CD\Leftrightarrow CD=\frac{4.\tan {{40}^{0}}}{\tan {{50}^{0}}-\tan {{40}^{0}}}=9,518m\) Tứ giác ADHF là hình chữ nhật (vì \(\overset{\hat{\ }}{\mathop{D}}\,=\overset{\hat{\ }}{\mathop{H}}\,=\overset{\hat{\ }}{\mathop{F}}\,={{90}^{0}}\)) \(\Rightarrow AF=DH=7m\) Vậy chiều cao CH của tòa nhà là: \(CH=CD+DH=9,518+7=16,518m\)







