Phương pháp giải:

Tìm m để \(y' \le 0,\,\,\forall x \in \left[ {1; + \infty } \right)\).

Lời giải chi tiết:

TXĐ: \(D = R\)

\(y' = m{x^2} + 14mx + 14\)

Hàm số nghịch biến trên nửa khoảng \(\left[ {1; + \infty } \right) \Leftrightarrow y' \le 0,\,\,\forall x \in \left[ {1; + \infty } \right)\)

\(\begin{array}{l} \Leftrightarrow m{x^2} + 14mx + 14 \le 0,\,\,\forall x \in \left[ {1; + \infty } \right) \Leftrightarrow m{x^2} + 14mx \le  - 14,\,\,\forall x \in \left[ {1; + \infty } \right)\\ \Leftrightarrow m\left( {{x^2} + 14x} \right) \le  - 14,\,\,\forall x \in \left[ {1; + \infty } \right) \Leftrightarrow m \le \dfrac{{ - 14}}{{{x^2} + 14x}},\,\,\forall x \in \left[ {1; + \infty } \right)\\\left( {Do\,\,{x^2} + 14x > 0\,\,\forall x \in \left[ {1; + \infty } \right)} \right)\end{array}\)

Xét hàm số \(f\left( x \right) = \dfrac{{ - 14}}{{{x^2} + 14x}},\,x \in \left[ {1; + \infty } \right)\):

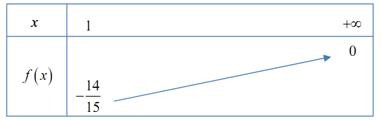
\(f'\left( x \right) = \dfrac{{28\left( {x + 7} \right)}}{{{{\left( {{x^2} + 14x} \right)}^2}}} > 0,\,\,\forall x \in \left[ {1; + \infty } \right) \Rightarrow \)Hàm số đồng biến trên \(\left[ {1; + \infty } \right)\)

Vậy với \(m \le  - \dfrac{{14}}{{15}}\) thì hàm số nghịch biến trên nửa khoảng \(\left[ {1; + \infty } \right)\).

Chọn: B