Câu hỏi
1) Hai lực song song cùng chiều cách nhau một đoạn 0,2 m. Biết một trong hai lực có độ lớn 13 N và hợp lực của chúng có giá cách lực còn lại một đoạn 0,08 m. Tính độ lớn của hợp lực và lực còn lại.
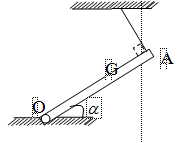
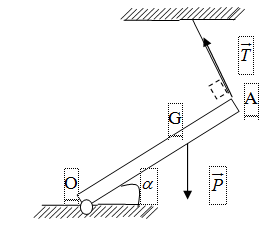
2) Cho thanh OA có đầu O gắn với bản lề trên sàn và đầu A được treo vào sợi dây mảnh nhẹ không giãn. Với G là trọng tâm của thanh GA = 1m, GO = 2m, = 300.
Biết lực căng trên dây có độ lớn là T = 10 N.
a) Tính trọng lượng của thanh.
b) Xác định hợp lực mà trục quay O tác dụng lên thanh.
Phương pháp giải:
pp động lực học
Lời giải chi tiết:
Sử dụng công thức tổng hợp hai lực song song cùng chiều, ta có:
Ta có: F1 = 13 N; d2 = 0,08 m; d1 = 0,2 – 0,08 = 0,12 (m);
\(\frac{{{F_2}}}{{{F_1}}}\) =\(\frac{{{d_1}}}{{{d_2}}}\)
=> F2 = F1 = 19,5 N. F = F1 + F2 = 32,5 N.
2)
a) Áp dụng điều kiện cân bằng của vật rắn quay quanh một trục cố đinh. Trục cố đinh ở đây đi qua tâm O. Ta có :
\(\begin{array}{l}
{M_P} = {M_T}\\
P.OGc{\rm{os}}\alpha = T.OA\\
P.2.c{\rm{os30 = 10}}{\rm{.3}}\\
{\rm{P = 10}}\sqrt {\rm{3}} \left( N \right)
\end{array}\)
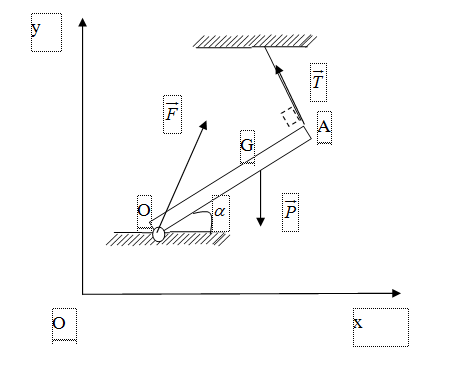
b) Gọi lực do trục quay O tác dụng lên thanh là F. ta có:
\(\vec P + \vec T + \vec F = \vec 0\left( 1 \right)\)
Ta có: Chọn hệ tọa độ Oxy với Ox nằm ngang sang phải, Oy thẳng đứng lên.
Chiếu (1) lên Ox ta được:
\({F_X} - T\sin \alpha = 0 \Rightarrow {F_X} = T\sin \alpha = 5\left( N \right)\)
Chiếu (1) lên Oy ta được:
\({F_y} - P + Tc{\rm{os}}\alpha = 0 \Rightarrow {F_y} = 5\sqrt 3 \left( N \right)\)
\(F = \sqrt {F_x^2 + F_y^2} = 10\left( N \right)\)
Do \(F_x^{};F_y^{}\) đều dương nên hướng chếch lên hợp với Ox một góc 600.