Phương pháp giải:

Phương pháp tìm GTLN, GTNN của hàm số \(y = f\left( x \right)\) trên \(\left[ {a;b} \right]\).

+) Giải phương trình \(y' = 0 \Rightarrow \) các nghiệm \({x_i} \in \left[ {a;b} \right]\).

+) Tính các giá trị \(f\left( a \right);\,\,f\left( b \right);\,\,f\left( {{x_i}} \right)\).

+) So sánh các giá trị tính được ở trên và kết luận.

Lời giải chi tiết:

\(y = {x^3} - 3{x^2} + m - 1 \Rightarrow y' = 3{x^2} - 6x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\)

Bảng biến thiên của hàm số trên đoạn \(\left[ {0;3} \right]\):

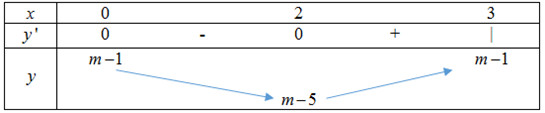
Để giá trị nhỏ nhất của hàm số \(y = {x^3} - 3{x^2} + m - 1\) trên đoạn \(\left[ {0;3} \right]\) bằng 2 thì \(m - 5 = 2 \Leftrightarrow m = 7\).

Chọn: B