Câu hỏi
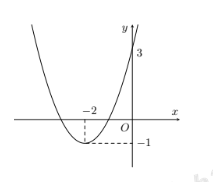
Hàm số nào sau đây có đồ thị như hình vẽ bên?
- A \(y = - 2{x^2} - 8x + 3\)
- B \(y = 2{x^2} + 8x + 3\)
- C \(y = - {x^2} - 4x + 3\)
- D \(y = {x^2} + 4x + 3\)
Phương pháp giải:
Gọi đồ thị hàm số là \(y = a{x^2} + bx + c\).
- Nếu \(a > 0\) thì đồ thị hàm số có bề lõm hướng lên trên, nếu \(a < 0\) thì đồ thị hàm số có bề lõm hướng xuống dưới.
- Đồ thị hàm số có đỉnh \(I\left( { - \dfrac{b}{{2a}}; - \dfrac{\Delta }{{4a}}} \right)\).
- Đồ thị hàm số cắt trục tung tại điểm \(\left( {0;c} \right)\).
Lời giải chi tiết:
Gọi đồ thị hàm số là \(y = a{x^2} + bx + c\).
Đồ thị hàm số có bề lõm hướng lên trên \( \Rightarrow a > 0 \Rightarrow \) Loại đáp án A và C.
Đồ thị hàm số cắt trục tung tại điểm có tung độ bằng 3 \( \Rightarrow c = 3\).
Đồ thị hàm số có đỉnh \(I\left( { - 2; - 1} \right)\)
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l} - \dfrac{b}{{2a}} = - 2\\ - \dfrac{{{b^2} - 12a}}{{4a}} = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} - 12a = 4a\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} = 16a\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 4a\\{b^2} = 4b\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}b = 0 \Rightarrow a = 0\,\,\left( {ktm} \right)\\b = 4 \Rightarrow a = 1\,\,\left( {tm} \right)\end{array} \right.\end{array}\)
Vậy \(y = {x^2} + 4x + 3\).
Chọn D.