Phương pháp giải:

a) Nhận thấy \(\left( {{d_1}} \right):y =  - 3x + 1\) và \(\left( {{d_2}} \right):y = x - 3\)là hai hàm số bậc nhất nên đồ thị của chúng có dạng đường thẳng. Để vẽ dạng đồ thị này, ta cần xác định hai điểm nằm trên đồ thị đó, sau đó kẻ đường thẳng đi qua hai điểm vừa xác định thì ta được đồ thị hàm số cần vẽ.

b) Tìm hoành độ giao điểm của hai đồ thị bằng cách lập phương trình hoành độ giao điểm, từ đó tìm ra tung độ của giao điểm , cuối cùng kết luận tọa độ giao điểm tìm được.

c) Hai đường thẳng song song với nhau khi chúng có cùng hệ số góc và hai đường thẳng đó không được trùng nhau.

Lời giải chi tiết:

a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng mặt phẳng tọa độ \(Oxy\).

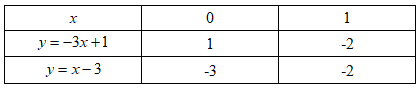
Ta có bảng giá trị:

Vậy đường thẳng \(\left( {{d_1}} \right)\) đi qua điểm \(\left( {0;\;1} \right),\;\;\left( {1; - 2} \right)\) và đường thẳng \(\left( {{d_2}} \right)\)  đi qua điểm \(\left( {0; - 3} \right),\;\;\left( {1; - 2} \right).\)

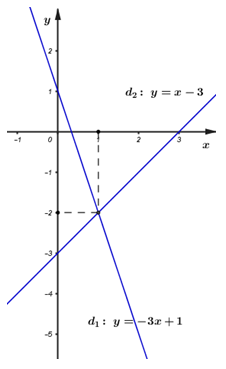
Từ đó ta có đồ thị của hai hàm số:

b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) bằng phép tính.

Hoành độ giao điểm của hai đường thẳng là nghiệm của phương trình :

\( - 3x + 1 = x - 3 \Leftrightarrow 4x = 4 \Leftrightarrow x = 1\).

Với \(x = 1 \Rightarrow y = x - 3 = 1 - 3 =  - 2\)

Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\)là: \(A\left( {1; - 2} \right)\).\(\)

c) Tìm \(m\) để đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\).

Hai đường thẳng song song khi chúng có cùng hệ số góc và chúng không trùng nhau. Suy ra để

đường thẳng \(\left( D \right):y = \left( {2m + 3} \right)x - 5\) song song với đường thẳng \(\left( {{d_1}} \right)\) thì:

\(\left\{ \begin{array}{l}2m + 3 =  - 3\\ - 5 \ne 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}2m =  - 6\\ - 5 \ne 1\end{array} \right. \Leftrightarrow m =  - 3\).

Vậy \(m =  - 3\) là giá trị cần tìm.

Chọn B.