Phương pháp giải:

1) Thay tọa độ điểm K vào hàm số để tìm a. Thay a tìm được vào hàm số và vẽ.

2) Xác định các điểm M, N và khoảng cách OM,  ON  theo a. Sử dụng công thức tính diện tích tam giác vuông và dữ kiện còn lại của đề bài để tìm a

Lời giải chi tiết:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng \(\left( d \right)\)\(:\,\,y = ax + 3\).

1) Xác định a biết \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\). Vẽ đồ thị với a vừa tìm được.

\(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\)\( \Rightarrow  - 1 = a.1 + 3 \Leftrightarrow a =  - 4\)

Vậy với \(a =  - 4\) thì \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\)

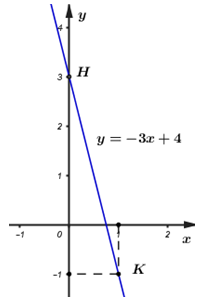
Với \(a =  - 4\) thì \(\left( d \right)\,:\,\,y =  - 4x + 3\)

Đường thẳng \(\left( d \right)\) đi qua \(K\left( {1; - 1} \right)\) và \(H\left( {0;3} \right)\)

2) Tìm tất cả các giá trị của a để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N sao cho diện tích tam giác OMN bằng 4.

Để đường thẳng \(\left( d \right)\) cắt Ox và Oy lần lượt tại hai điểm M và N \( \Leftrightarrow \,\,a \ne 0\)

\(M\left( {{x_M};{y_M}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Ox

\( \Rightarrow \left\{ \begin{array}{l}{y_M} = a{x_M} + 3\\{y_M} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_M} =  - \frac{3}{a}\\{y_M} = 0\end{array} \right. \Rightarrow M\left( { - \frac{3}{a};0} \right) \Rightarrow OM = \left| { - \frac{3}{a}} \right| = \left| {\frac{3}{a}} \right|\)

\(N\left( {{x_N};{y_N}} \right)\) là giao điểm của đường thẳng \(\left( d \right)\) và trục Oy

\( \Rightarrow \left\{ \begin{array}{l}{y_N} = a{x_N} + 3\\{x_N} = 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_N} = 0\\{y_M} = 3\end{array} \right. \Rightarrow N\left( {0;3} \right) \Rightarrow ON = 3\)

Diện tích tam giác OMN bằng 4 \( \Rightarrow {S_{\Delta OMN}} = \frac{1}{2}OM.ON = \frac{1}{2}.\left| {\frac{3}{a}} \right|.3 = \frac{9}{2}.\left| {\frac{1}{a}} \right| = 4 \Leftrightarrow \left| {\frac{1}{a}} \right| = \frac{8}{9} \Leftrightarrow \left| a \right| = \frac{9}{8} \Leftrightarrow \left[ \begin{array}{l}a = \frac{9}{8}\\a =  - \frac{9}{8}\end{array} \right.\)

Vậy với \(a = \frac{9}{8}\) hoặc \(a =  - \frac{9}{8}\) thỏa mãn yêu cầu đề bài.

Chọn A.