Câu hỏi
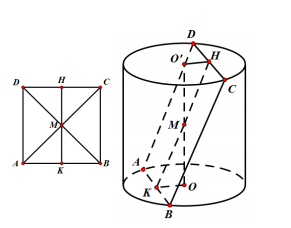
Cho hình trụ có trục \(OO' = 2\sqrt 7 \), ABCD là hình vuông có cạnh bằng 8 sao cho các đỉnh nằm trên đường tròn đáy và tâm hình vuông trùng với trung điểm OO’. Thể tích khối trụ là:
- A \(25\pi \sqrt 7 \)
- B \(50\pi \sqrt 7 \)
- C \(16\pi \sqrt 7 \)
- D \(25\pi \sqrt {14} \)
Phương pháp giải:
Sử dụng công thức tính thể tích khối trụ \(V = \pi {R^2}h\).
Lời giải chi tiết:
Gọi H, K lần lượt là trug điểm của AB và CD suy ra HK đi qua tâm của hình vuông ABCD và ta có \(MK = \frac{1}{2}AB = 4\).
OO’ là trục của hình trụ nên OO’ vuông góc với 2 mặt đáy.
\( \Rightarrow OO' \bot OK \Rightarrow OK = \sqrt {M{K^2} - M{O^2}} = 3\)
Vì K là trung điểm của AB \( \Rightarrow OK \bot AB\) (quan hệ vuông góc giữa đường kính và dây cung)
Xét tam giác vuông OKB \( \Rightarrow OB = \sqrt {O{K^2} + K{B^2}} = 5 = R\).
Vậy \(V = \pi {R^2}h = \pi {.5^2}.2\sqrt 7 = 50\pi \sqrt 7 \).
Chọn B.