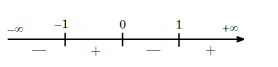Câu hỏi
Cho hàm số \(y = {x^4} - 2{x^2} + 1\) biết \(\left( {a;b} \right)\) là khoảng nghịch biến ngắn nhất của hàm số với \(a,b \in Z\). Tính giá trị của \(5a - b\) là:
- A -1
- B 6
- C -5
- D 2
Phương pháp giải:
Giải bất phương trình \(y' < 0\) tìm các khoảng nghịch biến của hàm số.
Lời giải chi tiết:
TXĐ : \(D = R\).
Ta có : \(y' = 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 1\\x = - 1\end{array} \right.\)
Bảng xét dấu : 
\( \Rightarrow \) Hàm số nghịch biến trên \(\left( { - \infty ; - 1} \right)\) và \(\left( {0;1} \right)\).
\( \Rightarrow \left( {0;1} \right)\) là khoảng nghịch biến cần tìm \( \Rightarrow a = 0;\,\,b = 1 \Rightarrow 5a - b = - 1\).
Chọn A.
Câu hỏi trước
