Câu hỏi
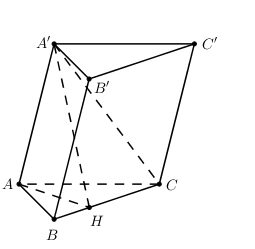
Cho hình lăng trụ ABC.A’B’C’ có \(AC = a\sqrt 3 ;\,\,BC = 3a;\,\,\widehat {ACB} = {30^0}\). Cạnh bên hợp với đáy một góc 600. Mặt phẳng \(\left( {A'BC} \right) \bot \left( {ABC} \right)\). Điểm \(H \in BC;\,\,BC = 3BH\) và mặt phẳng \(\left( {A'AH} \right) \bot \left( {ABC} \right)\). Tính theo a khoảng cách từ B đến \(\left( {A'AC} \right)\).
- A \(\frac{{3\sqrt 3 }}{4}a\)
- B \(\frac{{3a}}{4}\)
- C \(\frac{{a\sqrt 3 }}{4}\)
- D \(a\sqrt 3 \)
Phương pháp giải:
+) Xác định góc giữa cạnh bên và đáy.
+) \(d\left( {B;\left( {A'AC} \right)} \right)\).
Lời giải chi tiết:
Ta có: \(\left\{ \begin{array}{l}\left( {A'AH} \right) \bot \left( {ABC} \right)\\\left( {A'BC} \right) \bot \left( {ABC} \right)\\\left( {A'AH} \right) \cap \left( {A'BC} \right) = A'H\end{array} \right. \Rightarrow A'H \bot \left( {ABC} \right)\), khi đó góc giữa cạnh bên AA’ và mặt đáy (ABC) là \(\widehat {A'AH} = {60^0}\).
Ta lại có \(AH = \sqrt {C{H^2} + C{A^2} - 2CH.CA.\cos {{30}^0}} = a\)
Do đo \(A'H = AH\tan {60^0} = a\sqrt 3 \)
\( \Rightarrow {V_{ABC.A'B'C'}} = a\sqrt 3 \left( {\frac{1}{2}.3a.a\sqrt 3 \sin {{30}^0}} \right) = \frac{{9{a^3}}}{4}\).
\( \Rightarrow {V_{A'ABC}} = \frac{1}{3}{V_{ABC.A'B'C'}} = \frac{{3{a^3}}}{4}\).
Ta có: \(AC = a\sqrt 3 ;\,\,A'A = \frac{{AH}}{{\cos 60}} = 2a;\,\,A'C = \sqrt {{{\left( {2a} \right)}^2} + {{\left( {a\sqrt 3 } \right)}^2}} = a\sqrt 7 \)
\( \Rightarrow {S_{A'AC}} = \sqrt {p\left( {p - A'A} \right)\left( {p - A'C} \right)\left( {p - AC} \right)} \,\,\left( {p = \frac{{a\sqrt 3 + 2a + a\sqrt 7 }}{2}} \right) = {a^2}\sqrt 3 \).
Vậy \(d\left( {B;\left( {A'AC} \right)} \right) = \frac{{3{V_{A'.ABC}}}}{{{S_{A'AC}}}} = \frac{{3\sqrt 3 }}{4}a\).
Chọn A.