Câu hỏi
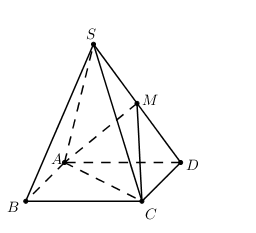
Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và M là trung điểm của SD. Biết rằng khối chóp S.ABCD có thể tích là a3 và tam giác MAC là tam giác đều cạnh a, hãy tính khoảng cách d từ điểm S đễn mặt phẳng (MAC).
- A \(d = \frac{{a\sqrt 3 }}{2}\)
- B \(d = \frac{{a\sqrt 3 }}{4}\)
- C \(d = \frac{{a\sqrt 3 }}{3}\)
- D \(d = a\sqrt 3 \)
Phương pháp giải:
\(d\left( {S;\left( {MAC} \right)} \right) = \frac{{3{V_{S.AMC}}}}{{{S_{MAC}}}}\)
Lời giải chi tiết:
Ta có: \(\frac{{{V_{S.AMC}}}}{{{S_{S.ADC}}}} = \frac{{SM}}{{SD}} = \frac{1}{2} \Rightarrow {V_{S.AMC}} = \frac{1}{2}{V_{S.ADC}}\).
Mà \({V_{S.ADC}} = \frac{1}{2}{V_{S.ABCD}} \Rightarrow {V_{SAMC}} = \frac{1}{4}{V_{S.ABCD}} = \frac{{{a^3}}}{4}\)
Tam giác MAC đều cạnh a \( \Rightarrow {S_{MAC}} = \frac{{{a^2}\sqrt 3 }}{4}\).
Vậy \(d\left( {S;\left( {MAC} \right)} \right) = \frac{{3{V_{S.AMC}}}}{{{S_{MAC}}}} = \frac{{3\frac{{{a^3}}}{4}}}{{\frac{{{a^2}\sqrt 3 }}{4}}} = a\sqrt 3 \).
Chọn D.
Câu hỏi trước
