Câu hỏi
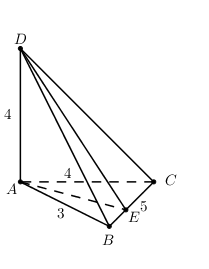
Cho tứ diện ABCD có \(AD \bot \left( {ABC} \right)\), \(AC = AD = 4;\,\,AB = 3;\,\,BC = 5\). Tính khoảng cách từ A đến mặt phẳng \(\left( {BCD} \right)\).
- A \(\frac{6}{{\sqrt {34} }}\)
- B \(\frac{4}{{\sqrt {34} }}\)
- C \(\frac{{12}}{{\sqrt {34} }}\)
- D \(\frac{5}{{\sqrt {34} }}\)
Phương pháp giải:
\(d\left( {A;\left( {BCD} \right)} \right) = \frac{{3{V_{ABCD}}}}{{{S_{BCD}}}}\)
Lời giải chi tiết:
Ta có: \(d\left( {A;\left( {BCD} \right)} \right) = \frac{{3{V_{ABCD}}}}{{{S_{BCD}}}}\)
Dễ thấy \(\Delta ABC\) vuông tại A (định lí Pytago đảo)
\( \Rightarrow AB \bot AC \Rightarrow {V_{ABCD}} = \frac{1}{6}AB.AC.AD = \frac{1}{6}.3.4.4 = 8\)
Kẻ \(AE \bot BC\) ta có: \(BC \bot \left( {SAE} \right) \Rightarrow BC \bot SE\).
Áp dụng hệ thức lượng trong tam giác vuông ABC có:
\(AE = \frac{{AB.AC}}{{BC}} = \frac{{3.4}}{5} = \frac{{12}}{5}\).
Áp dụng định lí Pytago trong tam giác vuông DAE có: \(DE = \sqrt {D{A^2} + A{E^2}} = \frac{{4\sqrt {34} }}{5}\).
\( \Rightarrow {S_{DBC}} = \frac{1}{2}DE.BC = \frac{1}{2}.\frac{{4\sqrt {34} }}{5}.5 = 2\sqrt {34} \)
Vậy \(d\left( {A;\left( {BCD} \right)} \right) = \frac{{24}}{{2\sqrt {34} }} = \frac{{12}}{{\sqrt {34} }}\).
Chọn C.