Câu hỏi
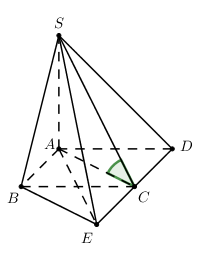
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với mặt phẳng (ABCD), góc giữa đường thẳng SC và mặt phẳng (ABCD) bằng 450. Tính khoảng cách giữa 2 đường thẳng SB và AC.
- A \(\dfrac{{a\sqrt {10} }}{5}\)
- B \(\dfrac{{2a\sqrt {10} }}{5}\)
- C \(\dfrac{{a\sqrt {10} }}{10}\)
- D \(a\sqrt {10} \)
Phương pháp giải:
+) Kẻ \(BE//AC\,\,\left( {E \in CD} \right)\) \( \Rightarrow AC//\left( {SBE} \right) \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\).
+) \(d\left( {A;\left( {SBE} \right)} \right) = \frac{{3{V_{S.ABE}}}}{{{S_{SBE}}}}\).
Lời giải chi tiết:
Kẻ \(BE//AC\,\,\left( {E \in CD} \right)\)
\( \Rightarrow AC//\left( {SBE} \right) \Rightarrow d\left( {AC;SB} \right) = d\left( {AC;\left( {SBE} \right)} \right) = d\left( {A;\left( {SBE} \right)} \right)\).
Dễ thấy ABEC là hình bình hành \( \Rightarrow BE = AC = a\sqrt 2 \).
\(\widehat {\left( {SC;\left( {ABCD} \right)} \right)} = \widehat {\left( {SC;AC} \right)} = \widehat {SCA} = {45^0} \Rightarrow \Delta SAC\) vuông cân tại A
\( \Rightarrow SA = AC = a\sqrt 2 \).
Xét tam giác vuông SAB có: \(SB = \sqrt {S{A^2} + A{B^2}} = \sqrt {2{a^2} + {a^2}} = a\sqrt 3 \).
Xét tam giác vuông ADE có: \(AE = \sqrt {A{D^2} + D{E^2}} = \sqrt {{a^2} + 4{a^2}} = a\sqrt 5 \)
Xét tam giác vuông SAE có: \(SE = \sqrt {S{A^2} + A{E^2}} = \sqrt {2{a^2} + 5{a^2}} = a\sqrt 7 \).
\( \Rightarrow {S_{SBE}} = \sqrt {\dfrac{{a\sqrt 3 + a\sqrt 2 + a\sqrt 7 }}{2}.\dfrac{{a\sqrt 2 + a\sqrt 7 - a\sqrt 3 }}{2}.\dfrac{{a\sqrt 3 + a\sqrt 2 - a\sqrt 7 }}{2}.\dfrac{{a\sqrt 3 + a\sqrt 7 - a\sqrt 2 }}{2}} = \dfrac{{{a^2}\sqrt 5 }}{2}\)
Ta có:
\({S_{ABE}} = \dfrac{1}{2}AB.d\left( {E;AB} \right) = \dfrac{1}{2}.a.a = \dfrac{1}{2}{a^2}\)
\( \Rightarrow {V_{S.ABE}} = \dfrac{1}{3}SA.{S_{ABE}} = \dfrac{1}{3}.a\sqrt 2 .\dfrac{{{a^2}}}{2} = \dfrac{{{a^3}\sqrt 2 }}{6}\).
Mà \({V_{S.ABE}} = \dfrac{1}{3}{S_{SBE}}.d\left( {A;\left( {SBE} \right)} \right) \Rightarrow d\left( {A;\left( {SBE} \right)} \right) = \dfrac{{3{V_{S.ABE}}}}{{{S_{SBE}}}} = \dfrac{{\frac{{{a^3}\sqrt 2 }}{2}}}{{\dfrac{{{a^2}\sqrt 5 }}{2}}} = \dfrac{{a\sqrt {10} }}{5}\)
Chọn A.