Phương pháp giải:

- Giản đồ Fres-nen

- Định lí hàm số sin trong tam giác

Lời giải chi tiết:

- Từ dữ kiện đề bài \({A_1} = 10cm;{\varphi _{x1}} = \varphi ;{\varphi _{x2}} =  - \frac{\pi }{2};{\varphi _x} =  - \frac{\pi }{3}\) ta vẽ được giản đồ vecto :

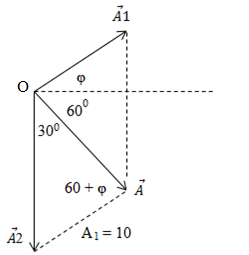
- Xét ∆OA₂A ta có: \(\left\{ \begin{array}{l}{A_2}A = {A_1} = 10cm\\\widehat {{A_2}OA} = {90^0} - {60^0} = {30^0}\\\widehat {OA{A_2}} = \widehat {{A_1}OA} = {60^0} + \varphi \,\,\,\left( {O{A_1}//{A_2}A} \right)\\\widehat {O{A_2}A} = {180^0} - \widehat {{A_2}OA} - \widehat {OA{A_2}} = {180^0} - {30^0} - {60^0} - \varphi  = {90^0} - \varphi \end{array} \right.\)

- Sử dụng định lí hàm số sin trong ∆OA₂A ta có:

\(\begin{array}{l}\frac{{{A_2}A}}{{\sin \widehat {{A_2}OA}}} = \frac{{O{A_2}}}{{\sin \widehat {OA{A_2}}}} = \frac{{OA}}{{\sin \widehat {O{A_2}A}}} \Leftrightarrow \frac{{10}}{{\sin 30}} = \frac{{{A_2}}}{{\sin \left( {60 + \varphi } \right)}} = \frac{A}{{\sin \left( {90 - \varphi } \right)}}\\ \Rightarrow \left\{ \begin{array}{l}A = \frac{{10.\sin \left( {90 - \varphi } \right)}}{{\sin 30}}\\{A_2} = \frac{{10.\sin \left( {60 + \varphi } \right)}}{{\sin 30}}\end{array} \right.\end{array}\)

- Năng lượng dao động cực đại khi \({A_{\max }} \Leftrightarrow \sin \left( {90 - \varphi } \right) = 1 \Leftrightarrow 90 - \varphi  = 90 \Rightarrow \varphi  = 0 \Rightarrow {A_2} = \frac{{10.\sin \left( {60 + 0} \right)}}{{\sin 30}} = 10\sqrt 3 cm\)