Phương pháp giải:

a) Lập bảng giá trị và vẽ đồ thị hàm số.

b) Tìm điểm\(A\left( {4;{y_0}} \right)\) là giao điểm của \(\left( {{d_3}} \right)\) và \(\left( {{d_2}} \right)\), \(\left( {{d_3}} \right)//\left( {{d_1}} \right)\) suy ra  a và dạng của \(\left( {{d_3}} \right)\), thay tọa độ điểm A vào đó để suy ra b

Lời giải chi tiết:

Cho hàm số \(y = 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\) và hàm số \(y =  - x + 3\) có đồ thị là \(\left( {{d_2}} \right)\).

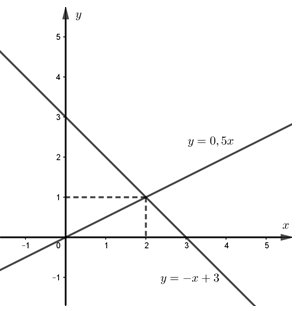
a) Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ Oxy.

\( \Rightarrow \left( {{d_1}} \right)\) là đường thẳng đi qua gốc tọa độ và điểm \(\left( {2;1} \right)\)

\( \Rightarrow \left( {{d_2}} \right)\) là đường thẳng đi qua 2 điểm \(\left( {0;3} \right)\) và \(\left( {3;0} \right)\)

b) Xác định các hệ số a, b của đường thẳng \(\left( {{d_3}} \right)\)\(:\,\,y = ax + b\). Biết \(\left( {{d_3}} \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( {{d_3}} \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có hoành độ bằng 4.

\(\left( {{d_3}} \right)//\left( {{d_1}} \right) \Leftrightarrow \left\{ \begin{array}{l}a = \frac{1}{2}\\b \ne 0\end{array} \right.\,\,\,\, \Rightarrow \,\,\left( {{d_3}} \right):\,\,y = \frac{1}{2}x + b\)

Gọi \(A\left( {4;{y_0}} \right)\) là giao điểm của \(\left( {{d_3}} \right)\) và \(\left( {{d_2}} \right)\)

\(A\left( {4;{y_0}} \right) \in \left( {{d_2}} \right) \Leftrightarrow {y_0} =  - 4 + 3 =  - 1 \Rightarrow A\left( {4; - 1} \right)\)

\(A\left( {4; - 1} \right) \in \left( {{d_3}} \right) \Leftrightarrow  - 1 = \frac{1}{2}.4 + b \Leftrightarrow  - 1 = 2 + b \Leftrightarrow b =  - 3\)  (tmđk \(b \ne 0\))

Vậy \(\left( {{d_3}} \right):y = \frac{1}{2}x - 3\)

Chọn B.