Câu hỏi
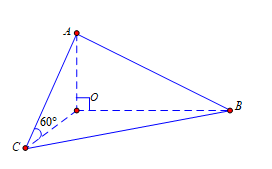
Cho tứ diện \(OABC\) có \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau. Biết \(OA = a\), \(OB = 2a\) và đường thẳng \(AC\) tạo với mặt phẳng \(\left( {OBC} \right)\) một góc \(60^\circ \). Thể tích khối tứ diện \(OABC\) bằng
- A \(\frac{{{a^3}\sqrt 3 }}{9}\).
- B \(3{a^3}\).
- C \({a^3}\).
- D \(\frac{{{a^3}\sqrt 3 }}{3}\).
Phương pháp giải:
Tứ diện OABC có OA, OB, OC đôi một vuông góc \( \Rightarrow {V_{OABC}} = \frac{1}{6}OA.OB.OC\).
Lời giải chi tiết:
Theo giả thiết \(OA\), \(OB\), \(OC\) đôi một vuông góc với nhau nên \(OA \bot \left( {OBC} \right)\), \(OC\) là hình chiếu của \(AC\) lên mặt phẳng \(\left( {OBC} \right)\). Do đó \(\widehat {ACO} = 60^\circ \), \(OA\) là chiều cao của tứ diện \(OABC\). Xét tam giác vuông \(AOC\) có \(\tan 60^\circ = \frac{{OA}}{{OC}}\) với \(OA = a\)
\( \Rightarrow OC = \frac{{OA}}{{\tan 60^\circ }} = \frac{a}{{\sqrt 3 }} = \frac{{a\sqrt 3 }}{3}\); \(OB = 2a\).
Ta có: \({S_{OBC}} = \frac{1}{2}OB.OC = \frac{1}{2}2a.\frac{{a\sqrt 3 }}{3} = \frac{{{a^2}\sqrt 3 }}{3}\); \({V_{OABC}} = \frac{1}{3}OA.{S_{OBC}} = \frac{1}{3}a.\frac{{{a^2}\sqrt 3 }}{3} = \frac{{{a^3}\sqrt 3 }}{9}\).
Chọn A.