Câu hỏi
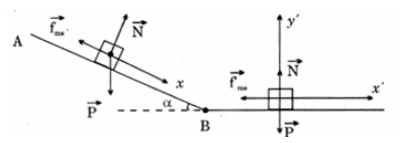
Một vật có khối lượng 100 kg trượt không ma sát không vận tốc đầu từ đỉnh một mặt phẳng nghiêng cao 5 m, nghiêng góc \(\alpha \)= 300 so với phương ngang. Lấy g = 10 m/s2.
1. Tìm khoảng thời gian vật chuyển động trên mặt phẳng nghiêng và vận tốc vật ở chân mặt phẳng nghiêng
2. Khi vật trượt hết mặt phẳng nghiêng, vật tiếp tục trượt chậm dần đều trên mặt phẳng ngang. Biết hệ số ma sát giữa vật và mặt phẳng ngang là \(\mu = \) 0,4. Tính thời gian và quãng đường vật đi được trên mặt phẳng ngang.
Phương pháp giải:
AH=h=5(m)
M=100kg
α=300
vA=0
g=10(m/s2)
tAB=? vB=? µBD=0,4tBD=? SBD=?
Lời giải chi tiết:
Phương trình động lực học: \(\vec N + \vec P = m\vec a\)
Chiếu phương trình véc tơ lên trục oy vuông góc với mặt phẳng nghiêng, chiều hướng lên trên ta được:
\( - mg.cos{30^0} + N = 0 = > Q = N = mg.cos30\)
Chiếu phương trình véc tơ lên trục ox song song với mặt phẳng nghiêng ta được
\(P.sin30{\rm{ }} = {\rm{ }}ma = > a = g.sin30 = 10.\frac{1}{2} = 5m/{s^2}\)
Áp dụng công thức \(v_B^2 - v_A^2 = 2a{S_{AB}}\)
Vì :
\(\left. {\begin{array}{*{20}{c}}
{\alpha = 30}\\
{h = 5\left( m \right)}
\end{array}} \right\}Canh\,huyen\,laAB = 10\left( m \right)\)
Ta có vì \({v_A} = 0\) nên ta có :
\({v_B} = \sqrt {2a{S_{AB}}} = \sqrt {2.5.10} = 10m/s\)
Thời gian vật chuyển động trên mặt phẳng nghiêng AB
\({v_B} = {v_0} + at = > {t_{AB}} = \frac{{{v_B} - {v_A}}}{a} = \frac{{10 - 0}}{5} = 2\left( s \right)\)
2. Vẽ hình trên phương ngang, phân tích lực tác dụng vào vật
Khi vật trượt trên mặt phẳng ngang có ma sát thì ta có phương trình ĐLH của vật là:
\({\vec F_{ms}} + \vec N + \vec P = m\vec a\)
Chiếu phương trình véc tơ lên trục oy vuông góc với mặt phẳng ngang BD và vuông góc với BD ta được
\( - P{\rm{ }} + {\rm{ }}N{\rm{ }} = {\rm{ }}0 = > P = N\)
Chiếu phương trình véc tơ lên trục 0X song song với mặt phẳng ngang BD ta được:
\( - {F_{ms}} = {\rm{ }}ma = > a = - \frac{{{F_{ms}}}}{m} = - \frac{{\mu mg}}{m} = - \mu g = > a = - 0,4.10 = - 4(m/{s^2})\)
Quãng đường vật đi được trên mặt phẳng ngang
ADCT: \(v_C^2 - v_B^2 = 2a{S_{BC}}\)
\( = > {S_{BC}} = \frac{{ - v_B^2}}{{2a}} = \frac{{ - {{10}^2}}}{{2.\left( { - 4} \right)}} = 12,5\left( m \right)\)
Thời gian vật đi được trên mặt phẳng ngang :
\({t_{BC}} = \frac{{{v_C} - {v_B}}}{a} = \frac{{0 - 10}}{{ - 4}} = 2,5\left( s \right)\)