Câu hỏi
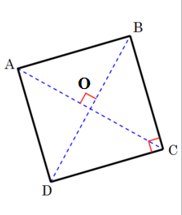
Cho hình vuông ABCD có tâm O. Trong các mệnh đề sau, tìm mệnh đề sai
- A \(\overrightarrow {AD} + \overrightarrow {DO} = - \frac{1}{2}\overrightarrow {CA} \)
- B \(\overrightarrow {AC} + \overrightarrow {DB} = 4\overrightarrow {AB} \)
- C \(\overrightarrow {AB} + \overrightarrow {AD} = 2\overrightarrow {AO} \)
- D \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CB} \)
Phương pháp giải:
Sử dụng công thức ba điểm và công thức hình bình hành.
Lời giải chi tiết:
+) \(\overrightarrow {AD} + \overrightarrow {DO} = \overrightarrow {AO} = - \frac{1}{2}\overrightarrow {CA} \).
+) \(\overrightarrow {AC} + \overrightarrow {DB} = 2\overrightarrow {AO} + 2\overrightarrow {OB} = 2\left( {\overrightarrow {AO} + \overrightarrow {OB} } \right) = 2\overrightarrow {AB} \)
\( \Rightarrow \overrightarrow {AC} + \overrightarrow {DB} = 4\overrightarrow {AB} \) là mệnh đề sai
+) \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} = 2\overrightarrow {AO} \).
+) \(\overrightarrow {OA} + \overrightarrow {OB} = \overrightarrow {CO} + \overrightarrow {OB} = \overrightarrow {CB} \).
Chọn: B