Câu hỏi
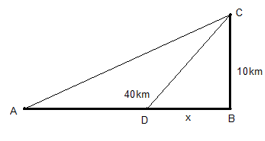
Một người cần đi từ khách sạn A bên bờ biển đến hòn đảo C. Biết rằng khoảng cách từ đảo C đến bờ biển là BC = 10km, khoảng cách từ khách sạn A đến điểm ngắn nhất tính từ đảo C vào bờ là AB = 40km. Người đó có thể đi đường thủy hoặc đi đường bộ rồi đi đường thủy từ khách sạn ra đảo (như hình vẽ dưới đây). Biết kinh phí đi đường thủy là 5 USD/km, kinh phí đi đường bộ là 3 USD/km. Hỏi người đó phải đi đường bộ một đoạn AD bao nhiêu để kinh phí đi từ A đến C nhỏ nhất? (AB vuông góc BC-hình dưới đây)
- A \(\frac{{15}}{2}\;\,km.\)
- B \(\frac{{65}}{2}\;\,km.\)
- C \(10\;\,km.\)
- D \(40\;\,km.\)
Phương pháp giải:
Lập hàm số tính kinh phí đi từ A đến C, với ẩn \(x = BD\).
Lời giải chi tiết:
Gọi độ dài đoạn BD là \(x\,\left( {km} \right),\,\,\left( {x \in \left[ {0;40} \right]} \right)\)
Khi đó, \(AD = 40 - x,\,\,DC = \sqrt {100 + {x^2}} \) (km)
Kinh phí đi từ A đến C: \(y = f\left( x \right) = 3\left( {40 - x} \right) + 5\sqrt {100 + {x^2}} \)
\(f'\left( x \right) = - 3 + \frac{{5x}}{{\sqrt {100 + {x^2}} }} = \frac{{ - 3\sqrt {100 + {x^2}} + 5x}}{{\sqrt {100 + {x^2}} }}\)
\(f'\left( x \right) = 0 \Leftrightarrow 3\sqrt {100 + {x^2}} = 5x \Leftrightarrow 900 + 9{x^2} = 25{x^2} \Leftrightarrow 16{x^2} = 900 \Leftrightarrow x = \frac{{15}}{2}\)
Ta có: \(f\left( 0 \right) = 170,\,\,f\left( {40} \right) = 50\sqrt {17} ,\,\,f\left( {\frac{{15}}{2}} \right) = 160\)
Vậy, kinh phí đi từ A đến C nhỏ nhất bằng 160USD khi \(BD = x = \frac{{15}}{2}\) (km).
Chọn: A