Câu hỏi
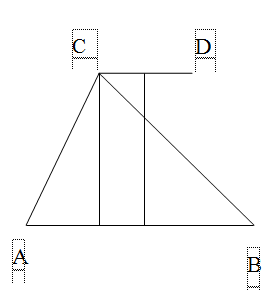
Tại hai điểm A và B trên mặt nước cách nhau 8cm có hai nguồn kết hợp dao động với phương trình: u1= u2 = acos40πt cm, tốc độ truyền sóng trên mặt nước là 30cm/s. Xét đoạn thẳng CD = 4cm trên mặt nước có chung đường trung trục với AB. Khoảng cách lớn nhất từ CD đến AB sao cho trên đoạn CD chỉ có 3 điểm dao động với biên độ cực đại là
- A 3,3cm
- B 8,9cm
- C 6cm.
- D 9,7cm
Phương pháp giải:
Sử dụng điều kiện cực đại trong giao thoa sóng nước
Lời giải chi tiết:
Bước sóng trong dao động :
\(\lambda = v.T = \frac{{v2\pi }}{\omega } = 1,5cm\)
Để CD có 3 cực đại thì C và D là hai cực đại bậc 1 và có 1 vân ở trên đường trung trực. Gọi khoảng cách từ CD đến AB là d
Điều kiện để C là cực đại bậc 1 là:
\(\begin{array}{l}
{d_1} - {d_2} = \lambda \\
\sqrt {{d^2} + {6^2}} - \sqrt {{d^2} + {2^2}} = 1,5\\
\Leftrightarrow \sqrt {{d^2} + {6^2}} = 1,5 + \sqrt {{d^2} + {2^2}} \\
\Leftrightarrow {d^2} + {6^2} = 1,{5^2} + {d^2} + {2^2} + 3.\sqrt {{d^2} + {2^2}} \\
\Leftrightarrow \frac{{119}}{{12}} = \sqrt {{d^2} + {2^2}} \\
\Leftrightarrow d = 9,7cm
\end{array}\)