Câu hỏi
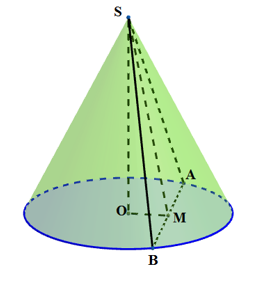
Cho khối nón đỉnh \(O\) trục \(OI\), bán kính đáy bằng a và chiều cao bằng \(\frac{a}{2}\). Mặt phẳng \(\left( P \right)\) thay đổi luôn đi qua O và cắt hình nón theo thiết diện là tam giác AOB. Diện tích lớn nhất của tam giác AOB là:
- A \(\frac{{{a^2}}}{2}\).
- B \(\frac{{3{a^2}}}{4}\).
- C \(\frac{{3{a^2}}}{8}\).
- D \(\frac{{5{a^2}}}{8}\).
Phương pháp giải:
Gọi M là trung điểm của AB \( \Rightarrow SM \bot AB \Rightarrow {S_{\Delta SAB}} = \frac{1}{2}SM.AB\)
Lời giải chi tiết:
Gọi M là trung điểm của AB và độ dài đoạn OM là x
\(\Delta SOM\) vuông tại O \( \Rightarrow SM = \sqrt {S{O^2} + O{M^2}} = \sqrt {\frac{{{a^2}}}{4} + {x^2}} \)
\(\Delta BOM\) vuông tại M \( \Rightarrow BM = \sqrt {O{B^2} - O{M^2}} = \sqrt {{a^2} - {x^2}} \) \( \Rightarrow AB = 2\sqrt {{a^2} - {x^2}} \)
Ta có: \(AB \bot OM,\,\,AB \bot SO \Rightarrow AB \bot \left( {SOM} \right) \Rightarrow AB \bot SM\)
\( \Rightarrow {S_{\Delta SAB}} = \frac{1}{2}.SM.AB = \frac{1}{2}.\sqrt {\frac{{{a^2}}}{4} + {x^2}} .2\sqrt {{a^2} - {x^2}} = \sqrt {\frac{{{a^2}}}{4} + {x^2}} .\sqrt {{a^2} - {x^2}} \le \frac{{\left( {\frac{{{a^2}}}{4} + {x^2}} \right) + \left( {{a^2} - {x^2}} \right)}}{2} = \frac{{5{a^2}}}{8}\)
Diện tích lớn nhất của tam giác AOB là: \(\frac{{5{a^2}}}{8}\).
Chọn: D