Câu hỏi
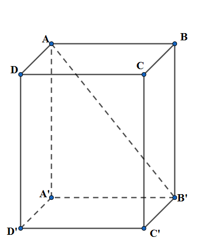
Cho hình lăng trụ đứng \(ABCD.A'B'C'D'\) có đáy là hình vuông cạnh bằng 3, đường chéo AB’ của mặt bên \(\left( {ABB'A'} \right)\) có độ dài bằng 5. Tính thể tích V của khối lăng trụ \(ABCD.A'B'C'D'\).
- A \(V = 36\).
- B \(V = 48\).
- C \(V = 18\).
- D \(V = 45\).
Phương pháp giải:
Thể tích của khối lăng trụ: \(V = Sh\).
Lời giải chi tiết:
\(\Delta ABB'\) vuông tại B \( \Rightarrow BB' = \sqrt {AB{'^2} - A{B^2}} = \sqrt {{5^2} - {3^2}} = 4\)
Thể tích V của khối lăng trụ \(ABCD.A'B'C'D'\):
\(V = {S_{ABCD}}.BB' = {3^2}.4 = 36\).
Chọn: A
Câu hỏi trước
