Câu hỏi
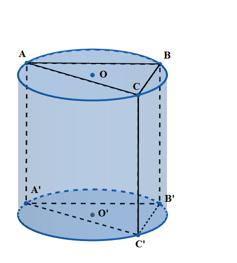
Cho lăng trụ tam giác đều tất cả các cạnh bằng a. Một hình trụ tròn xoay có hai đáy là hai hình tròn ngoại tiếp hai đáy của lăng trụ. Thể tích của khối trụ tròn xoay bằng:
- A \(\frac{{\pi {a^3}}}{9}\).
- B \(\pi {a^3}\).
- C \(3\pi {a^3}\).
- D \(\frac{{\pi {a^3}}}{3}\).
Phương pháp giải:
Thể tích khối trụ: \(V = \pi {r^2}h\).
Lời giải chi tiết:
\(\Delta ABC\) đều cạnh a \( \Rightarrow \) Bán kính đường tròn ngoại tiếp tam giác ABC: \(r = \frac{2}{3}.\frac{{a\sqrt 3 }}{2} = \frac{a}{{\sqrt 3 }}\)
Thể tích của khối trụ tròn xoay là: \(V = \pi {r^2}h = \pi .{\left( {\frac{a}{{\sqrt 3 }}} \right)^2}.a = \frac{{\pi {a^3}}}{3}\).
Chọn: D
Câu hỏi trước
