Câu hỏi
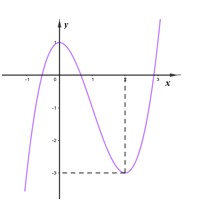
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị trong hình bên. Hỏi phương trình \(a{x^3} + b{x^2} + cx + d + 2 = 0\) có bao nhiêu nghiệm?
- A Phương trình có đúng một nghiệm.
- B Phương trình có đúng hai nghiệm.
- C Phương trình không có nghiệm.
- D Phương trình có đúng ba nghiệm
Phương pháp giải:
Số nghiệm của phương trình \(a{x^3} + b{x^2} + cx + d + 2 = 0\) bằng số giao điểm của đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) và đường thẳng \(y = - 2\)
Lời giải chi tiết:
Số nghiệm của phương trình \(a{x^3} + b{x^2} + cx + d + 2 = 0\) bằng số giao điểm của đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) và đường thẳng \(y = - 2\)
Quan sát đồ thị hàm số, ta thấy : đồ thị hàm số \(y = a{x^3} + b{x^2} + cx + d\) cắt đường thẳng \(y = - 2\) tại 3 điểm phân biệt \( \Rightarrow \) Phương trình đã cho có đúng ba nghiệm.
Chọn: D