Câu hỏi
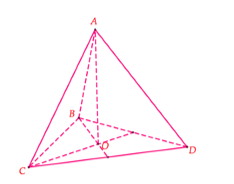
Cho hình chóp \(S.ABC\) có \(SA = a,\,\,SB = b,\,SC = c\) và \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0}\). Tính thể tích của khối chóp \(S.ABC\).
- A \(\frac{{\sqrt 2 }}{{12abc}}\).
- B \(\frac{{\sqrt 2 }}{{12}}abc\).
- C \(\frac{{\sqrt 2 }}{4}abc\).
- D \(\frac{{\sqrt 2 }}{{4abc}}\).
Phương pháp giải:
Thể tích của khối tứ diện đều cạnh bằng a : \(V = \frac{{\sqrt 2 {a^3}}}{{12}}\).
Lời giải chi tiết:
Không mất tính tổng quát, giả sử \(a = \min \left\{ {a;\,b;\,c} \right\}\)
Trên cạnh SB, SC lần lượt lấy các điểm B’, C’ sao cho \(SB' = SC' = SA = a\)
Khi đó, do \(\widehat {ASB} = \widehat {BSC} = \widehat {CSA} = {60^0}\) nên tứ diện \(S.AB'C'\) là tứ diện đều và \({V_{S.AB'C'}} = \frac{{\sqrt 2 {a^3}}}{{12}}\)
Ta có: \(\frac{{{V_{S.AB'C'}}}}{{{V_{S.ABC}}}} = \frac{{SB'}}{{SB}}.\frac{{SC'}}{{SC}} = \frac{a}{b}.\frac{a}{c} = \frac{{{a^2}}}{{bc}} \Rightarrow {V_{S.ABC}} = \frac{{{V_{S.AB'C'}}}}{{\frac{{{a^2}}}{{bc}}}} = \frac{{\frac{{\sqrt 2 {a^3}}}{{12}}}}{{\frac{{{a^2}}}{{bc}}}} = \frac{{\sqrt 2 abc}}{{12}}\).
Chọn: B