Phương pháp giải:

+) Rút z theo w, tìm tập hợp các điểm biểu diễn số phức w.

+) Biểu diễn hình học tất cả các yếu tố có trong bài toán.

+) Tìm điều kiện để P đạt giá trị lớn nhất.

Lời giải chi tiết:

\(z + w = 3 + 4i \Rightarrow z = 3 + 4i - w \Rightarrow \left| {3 + 4i - 2w} \right| = 9 \Leftrightarrow \left| {w - \frac{3}{2} - 2i} \right| = \frac{9}{2}\)

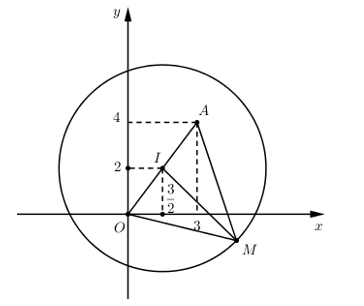
Khi đó tập hợp các điểm biểu diễn số phức w là đường tròn tâm \(I\left( {\frac{3}{2};2} \right)\) bán kính \(R = \frac{9}{2}\).

Ta có: \(T = \left| z \right| + \left| w \right| = \left| {w - 3 - 4i} \right| + \left| w \right|\)

Gọi M là điểm biểu diễn số phức w, \(A\left( {3;4} \right)\) là điểm biểu diễn số phức \(z = 3 + 4i\). Dễ thấy I là trung điểm của OA.

Khi đó \(P = MO + MA\)

\({P_{\max }} \Leftrightarrow OM = OA \Leftrightarrow MI \bot OA\).

Ta có: \(OI = \sqrt {\frac{9}{4} + 4}  = \frac{5}{2}\), \(IM = R = \frac{9}{2}\)

\( \Rightarrow OM = \sqrt {\frac{{25}}{4} + \frac{{81}}{4}}  = \frac{{\sqrt {106} }}{2}\)

\( \Rightarrow {P_{\max }} = 2OM = \sqrt {106} \).

Chọn đáp án D.