Phương pháp giải:

Chia trường hợp của m và tìm GTLN của hàm số trong từng trường hợp đó.

Lời giải chi tiết:

ĐK: \(x \ne  - m\)

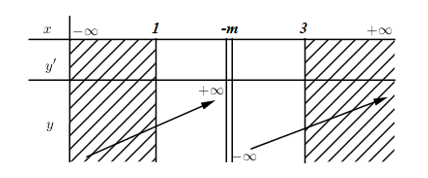
\(y' = \frac{{{m^2} + 1}}{{{{\left( {x + m} \right)}^2}}} > 0\,\,\forall x \ne  - m \Rightarrow \) Hàm số đồng biến trên \(\left( { - \infty ; - m} \right)\) và \(\left( { - m; + \infty } \right)\)

TH1: \(1 < 3 <  - m \Rightarrow \mathop {\max }\limits_{\left[ {1;3} \right]} y = y\left( 3 \right) = \frac{{3m - 1}}{{3 + m}} = 2 \Leftrightarrow 3m - 1 = 2m + 6 \Leftrightarrow m = 7\,\,\left( {ktm} \right)\)

TH2: \( - m < 1 < 3 \Rightarrow \mathop {\max }\limits_{\left[ {1;3} \right]} y = y\left( 3 \right) = \frac{{3m - 1}}{{3 + m}} = 2 \Leftrightarrow 3m - 1 = 2m + 6 \Leftrightarrow m = 7\,\,\left( {tm} \right)\)

TH3: \(1 <  - m < 3\)

TH này không tồn tại GTLN của hàm số trên \(\left[ {1;3} \right]\).

Vây \(m = 7\).

Chọn đáp án B.