Phương pháp giải:

a) Parabol \(\left( P \right):\,\,y = a{x^2} + bx + c\,,\,\left( {a \ne 0} \right)\) nhận \(x =  - \frac{b}{{2a}}\) làm trục đối xứng và có đỉnh \(I\left( { - \frac{b}{{2a}};\frac{{{b^2} - 4ac}}{{4a}}} \right)\).

b) Hàm số\(y = a{x^2} + bx + c\,\) có \(a > 0\), đồng biến trên khoảng \(\left( { - \frac{b}{{2a}}; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - \frac{b}{{2a}}} \right)\).

Lời giải chi tiết:

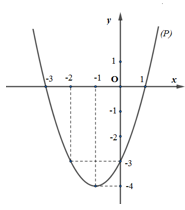
a) Xác định trục đối xứng và tọa độ đỉnh của parabol \(\left( P \right)\). Vẽ parabol \(\left( P \right)\).

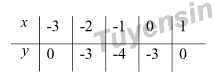
Parabol \(\left( P \right):\,\,y = {x^2} + 2x - 3\) nhận \(x =  - 1\) làm trục đối xứng và có đỉnh \(I\left( { - 1; - 4} \right)\)

Một số điểm trên (P):

Đồ thị hàm số (hình bên):

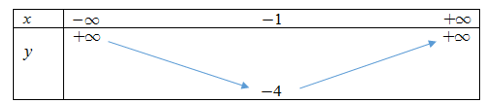
b) Xác định khoảng đồng biến, khoảng nghịch biến và lập bảng biến thiên của hàm số \(y = {x^2} + 2x - 3\).

Hàm số\(y = {x^2} + 2x - 3\) có \(1 > 0\), đồng biến trên khoảng \(\left( { - 1; + \infty } \right)\) và nghịch biến trên khoảng \(\left( { - \infty ; - 1} \right)\).

Bảng biến thiên của hàm số \(y = {x^2} + 2x - 3\)